이진 탐색 트리 (Binary Search Trees)-2장
on
이진 탐색 트리 (Binary Search Trees) - 2부
이진 탐색 트리에서 원소 삭제
- 키(key)를 이용해서 노드를 찾는다
- 만약 해당 키의 노드가 없으면 삭제할 것이 없음
- 노드가 있으면 찾은 노드의 부모 노드도 알고 있어야 함
- 찾은 노드를 제거하고도 이진 탐색 트리 성질을 만족하도록 트리의 구조를 정리
인터페이스 설계
입력: 키 (Key)
출력: 삭제한 경우 True, 해당 키의 노드가 없는 경우 False
class Node:
def remove(self, key):
node, parent = self.lookup(key)
if node:
return True
else:
return False
이진 탐색 트리 구조의 유지
삭제되는 노드가
-
말단(leaf) 노드 인경우
-
그냥 그 노드를 없애면 됨
-> 부모 노드의 링크를 조정(좌? 우?를 판단후)
-
-
자식을 하나 가지고 있는 경우
- 자식이 왼쪽? 오른쪽 판단(자식을 삭제된 노드 위치로 붙히기 위해)
- 부모의 노드의 링크를 조정(좌, 우 판단)
-
자식을 둘 가지고 있는 경우
- 삭제되는 노드보다 바로 다음 (큰) 키를 가지는 노드를 찾아 그 노드를 삭제되는 노드 자리에 대신 배치하고 이 노드를 대신 삭제
우선 자식을 세어 보자
특정한 노드가 몇 개의 자식을 갖고 있는지 세어 보는 코드를 작성
class Node:
def countChildren(self):
count = 0
if self.left:
count += 1
if self.right:
count += 1
return count
밑단 노드(leaf)의 삭제
가장 간단한 단계인 leaf 노드를 삭제하는 경우를 살펴 보자. 부모노드를 P, 삭제 하려는 노드를 X라고 표시 했다. X가 P노드의 왼쪽자식, 오른쪽 자식인 경우가 존재 한다. 이런 경우, 그냥 X라는 노드를 삭제하면 되기 때문에 P노드만 남게 된다.

lookup 메소드를 통해 P노드를 알아내고. 왼쪽, 오른쪽 인지 여부를 파악하고 None 값을 대입한다.
삭제된는 노드(X)가 root node인 경우?
노드가 1개 임으로, 트리 전체가 삭제 된다.
예제
노드 X의 부모 노드인 P를 찾고 오른쪽을 None 으로 만들면 노드를 삭제 할 수 있다. 중요한 점은 삭제후에도 이진 탐색 트리 성질을 만족 한다는 것이다.(왼쪽 서브 트리가 자기 자신보다 작고 오른쪽은 큰)

자식이 하나인 노드 삭제
노드 X를 삭제 하고자 한다. 그림과 같이 C노드(자식 한개)를 갖고 있는 형태 이다. X를 삭제 해도 이진 탐색 트리 성질을 만족하게 된다. 그냥 X노드를 삭제하고 그 자리에 C를 집어 넣어 주면 된다. 단, 자식이 왼쪽, 오른쪽인지 여부를 파악하고 붙혀야 한다. 그렇기 때문에 P를 찾아 왼쪽인지 오른쪽인지 알고 있어야 한다.

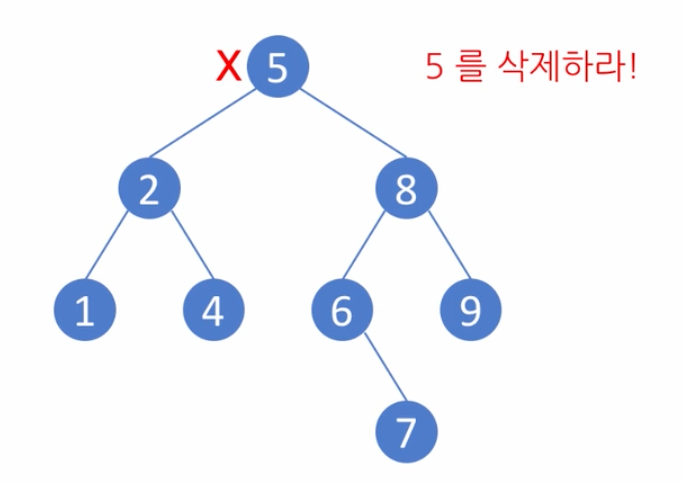
삭제되는 node가 root node인 경우
대신 들어오는 자식이 새로 root가 된다.
예제
X 노드를 삭제하기 이전에 부모 노드인 P에 어느쪽(오른쪽, 왼쪽)에 있는지를 파악하고, 그 자리에 C를 붙혀 넣는다.
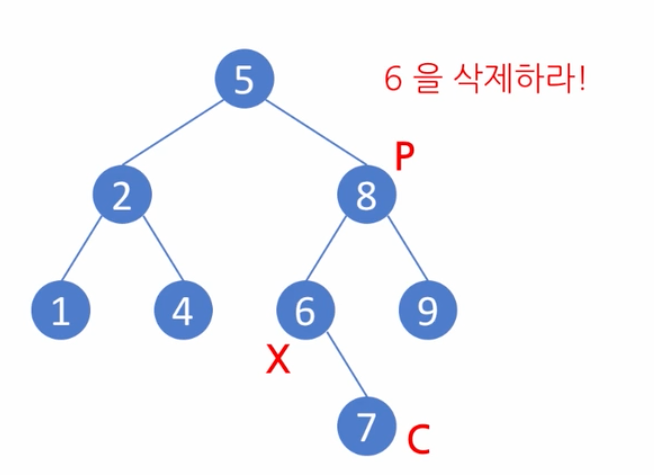
자식이 둘인 노드의 삭제
예제1
S가 왼쪽에서 발견
노드 5의 경우 자식이 2와 8로 두 개인 경우이다. 5보다 한단계 큰 노드를 찾아서 대신 가져다 놔야 한다. 그런 노드를 찾아야 한다.
즉, 오른쪽 Subtree에서 가장 작은 노드를 찾아야 한다. 이를 S라고 표현하고, S에 대한 부모를 P라고 한다.
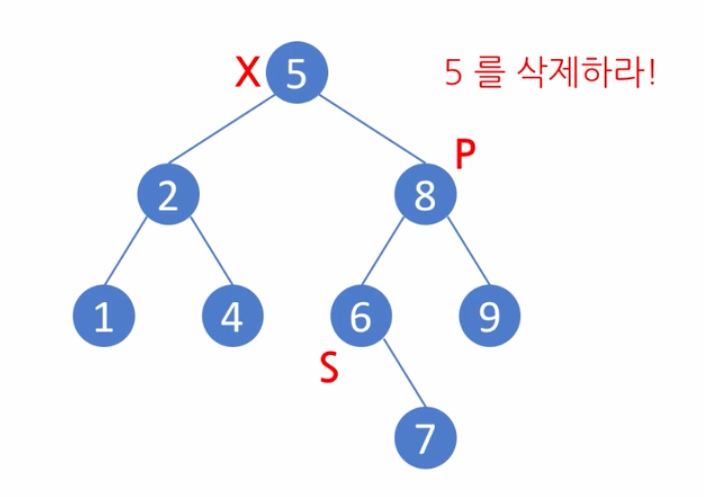
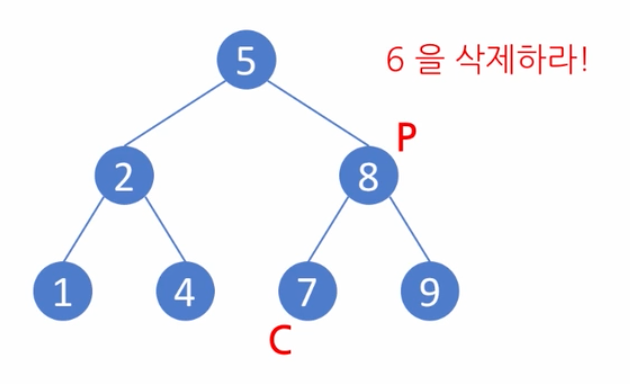
찾은 S를 X로 대체하고, 기존의 6(S)를 삭제한다.
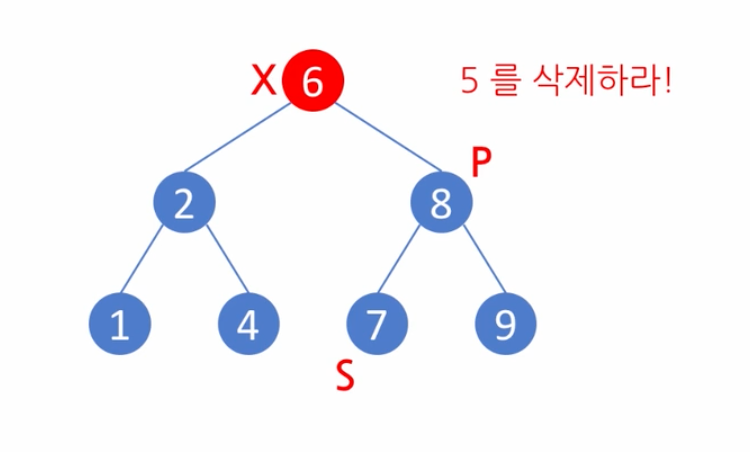
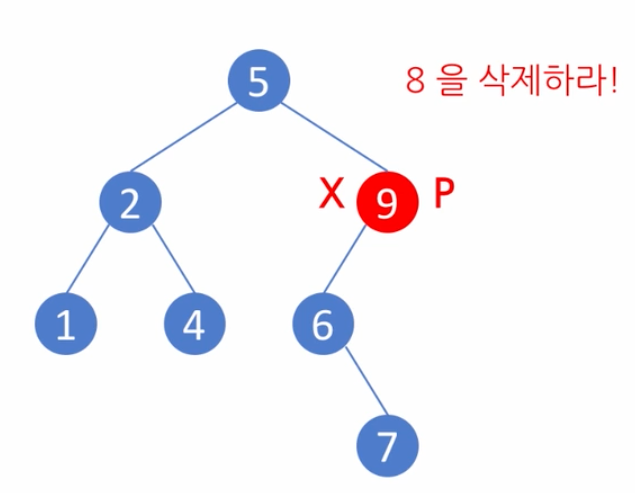
예제2
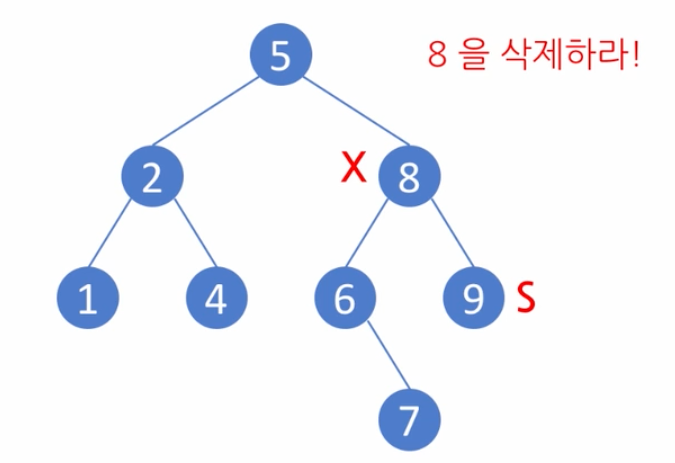
S가 오른쪽에서 발견
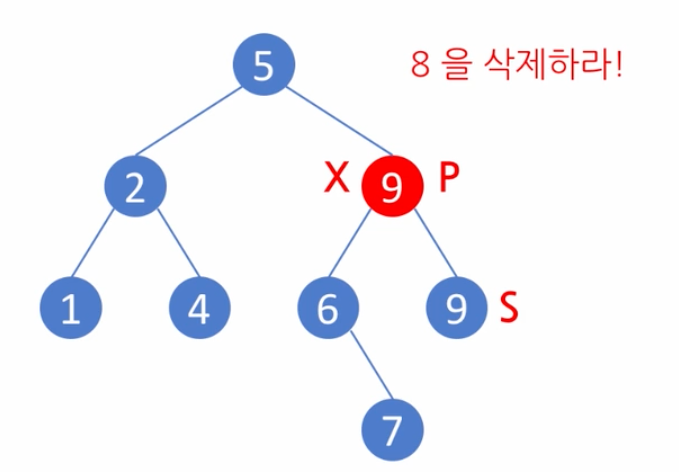
이번에는 8을 삭제하는 경우에 조금 달라진다. 8에서 한단계 큰 노드인 9를 S라고 한다. 위와 같이 S의 부모를 P라고 하면 P와 X가 같게된다 P==X.
예제1에서는 P노드 기준 왼쪽 노드를 제거 했지만, S가 왼쪽에서 발견되는 경우, P의 오른쪽을 삭제 한다.
이진탐색트리가 비효울적이지 못한 경우
- 순서대로 삽입하는 경우 효율적이지 못하다
- 한쪽으로 치우치는 모양
이런 경우, 선형 탐색과 동일한 구조를 갖게 된다. 이럴경우 $logn$의 탐색 복잡도를 갖을 수 없게 된다