[베이즈 통계학] 최대우도법(MLE)과 최대사후법(MAP) 이해하기

Written by metterian
on 

이항분포(Binomial Distribution)

이항 분포란 연속적(continuos)하지 않고 이산적(discrete)한 분포에 대해 이항분포라고 표현합니다. 여기서 이산적이란 표현은 동전 던지기를 할 때 처럼 앞/뒤 와 같이 정해진 케이스만 존재하는 경우를 말합니다.

또한, 동전 던지기와 같은 실험을 베르누이(Bernoulli) 시행(실험)이라고 표현합니다.

i.i.d(Independent & Identically distributed)

이러한 동전 던지기를 할 때는 i.i.d(Independent & Identically distributed)를 가정하게 됩니다.

독립적(Independent)라는 의미는 동전 던지기를 할 때 앞에서 던진 행위와 지금 던지는 행위가 전혀 관계가 없다는 의미 입니다.

동일한(Identically)의 의미는 동전 던지기를 계속 시행하면서 동전에 아무러 손상이 없어 계속해서 앞/뒤가 나올 확률이 동일한 상태를 의미합니다.

예제

다음과 같이 앞면이 나올 확률을 $H$라고 확률변수를 설정해 봅시다. 그러면 다음과 같은 수식을 표현 할 수 있습니다.

예를 들어, 동전던지기를 5회 시행하여 ‘앞앞뒤앞뒤’와 같은 결과가 나왔다고 가정해 봅시다. 이는 다음과 같은 수식으로 표현 가능 합니다.

\[\begin{aligned} P(HHTHT) &= \theta\theta(1-\theta)\theta(1-\theta)\\ &= \theta^{3}(1-\theta)^2 \end{aligned}\]

각 시행은 서로 독립 사건이기 때문에 확률의 곱으로 표현이 가능합니다.


이항분포 식

위의 주어진 예시를 바탕으로 동전던지기 시행의 결과를 $D(data)$라고 표현 해봅니다. 그리고 주어진 예시를 일반화 하게 되면 다음과 같은 수식으로 나타낼 수 있습니다.

\[\begin{aligned} D &= {H,H,T,H,T}\\ k& = a_H = 3\\ p& = \theta\\ \end{aligned}\]

위의 식에서 $a_H$는 앞면이 나온 횟수를 의미하고 $p$의 의미는 H(앞면)이 나올 확률을 의미합니다. 이를 다음과 같은 식으로 나타 낼 수 있습니다.

\[P(D \mid \theta) = \theta^{a_H}(1-\theta)^{a_r}\\\]

위의 식에서 $\theta$가 주어졌을 때 해당 데이터 셋 $D$가 발생할 확률은 $P(D \mid \theta)$로 나타낼 수 있습니다. 또한 위의 식에서 $\alpha_{H}, \alpha_{T}$는 데이터셋 $D$에서 머리(H)와 꼬리(T)가 각각 발생한 횟수입니다.

그렇다면 순서에 상관없이 머리와 꼬리가 나타날 확률은 어떻게 구할 수 있을까요? 위에서 나타냈던 특정 한 사건(여기서는 머리)이 발생할 확률 θ 를 p로, 그 사건이 $a_H$ 를 $k$ 로 바꿔줍시다. 그러면 임의의 순서대로 구성된 $n$ 개의 사건 세트에서 발생할 확률이 $p$ 인 특정 한 사건이 $k$ 번 나올 확률을 아래와 같은 함수 $f$ 로 나타낼 수 있습니다.

\[\begin{array}{c} f(k ; n, p)=P(K=k)=\left(\begin{array}{l} n \\ k \end{array}\right) p^{k}(1-p)^{n-k} \\ \because\left(\begin{array}{c} n \\ k \end{array}\right)=\frac{n !}{k !(n-k) !} \end{array}\]


최대우도법(Maximum Likelihood Estimation)

확률이 주어졌을 때, 데이터가 관측 될 확률을 다음과 같이 나타내었습니다.

\[P(D \mid \theta)=\theta^{a_{H}}(1-\theta)^{a_{T}}\]


최대우도법(MLE)

MLE(Maximum Likelihood Estimation) of $\theta$

다음과 같이 5개의 데이터를 얻었다고 가정해 봅시다.

\[x=\{1,4,5,6,9\}\]

이 때, 아래의 그림을 봤을 때 $x$ 는 주황색 확률분포와 파란색 확률분포 중 어떤 확률분포으로부터 추출되었을 확률이 더 높을 까요?

pic1

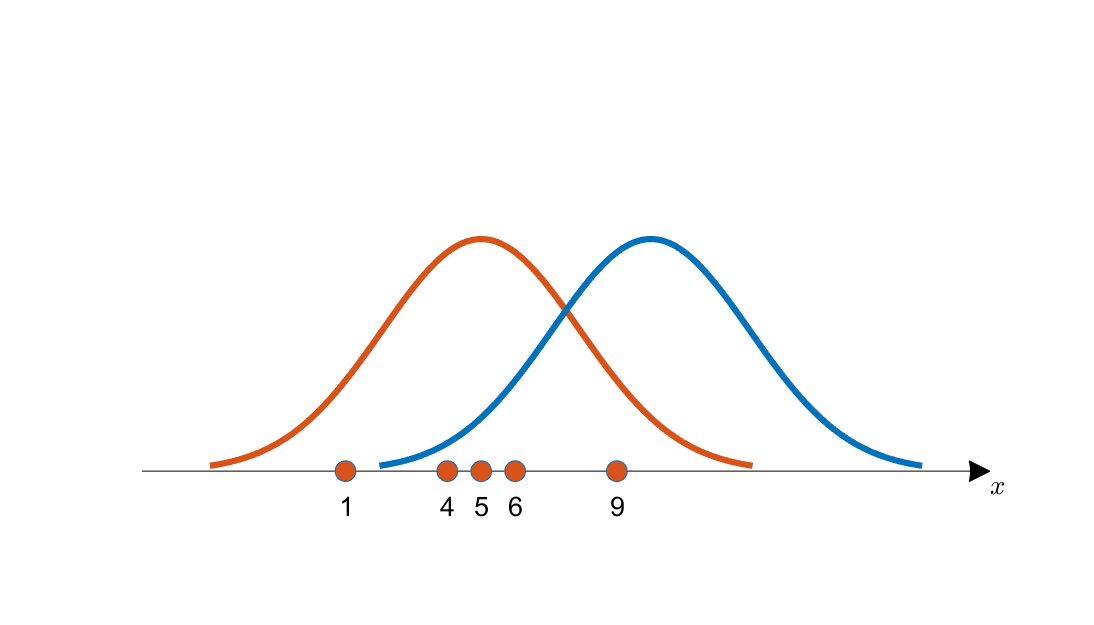
눈으로 보기에도 파란색 분포 보다는 주황색 분포에서의 확률이 추출 되었을 가능성이 높을 것입니다. 즉, 주황색 분포는 파란색 분포에 비해 가능도(likelihood, 우도)가 높다고 이야기 할 수 있습니다. 이러한 가장 큰 우도를 찾는 기법을 최대 우도법이라고 합니다.

최대우도법이랑 관측 데이터로 부터 가장 잘 표현되는 후보 확률 분포 중에서 최적의 확률 분포를 찾아해는 기법을 이야기 합니다.

\[\hat{\theta}=\operatorname{argmax}_{\theta} P(D \mid \theta)\]


MLE 계산

MLE를 계산하기 위해서는 자승들을 곱해서 계산해야 합니다. 하지만 이럴 경우 계산이 복잡해지는 단점이 있기 때문에 계산식에 $log$ 함수를 사용하여 이를 계산합니다.

\[\hat{\theta}=\operatorname{argmax}_{\theta} P(D \mid \theta) = \operatorname{argmax}_{\theta} \theta^{a_{H}}(1-\theta)^{a_{T}}\]

로그 함수의 사용

위의 식을 로그 함수로 매핑을 시켜도 최대 최소가 유지됩니다. 즉, 우리가 MLE 값이 최대가 되는 지점을 찾기위해 log함수를 사용하여도 된다는 의미입니다.

\[\begin{array}{c} \hat{\theta}=\operatorname{argmax}_{\theta} \ln P(D \mid \theta)=\operatorname{argmax}_{\theta} \ln \left\{\theta^{a_{H}}(1-\theta)^{a_{T}}\right\} \\ =\operatorname{argmax}_{\theta}\left\{a_{H} \ln \theta+a_{T} \ln (1-\theta)\right\} \end{array}\]

$log$ 함수를 사용하면 함수값이 변화하게 되지만 최대 지점은 변화하지 않기 때문에 최대지점을 찾기 위한 목표로 사용이 가능한 것이지요.

위의 수식에서 $\theta$를 최대화 하는 수식을 풀면 확률분포가 최대가 되는 지점을 찾을 수 있습니다.

미분을 이용한 최댓값 찾기

최대화 문제를 풀기위해서 미분을 사용해서 최대지점을 다음과 같이 찾을 수 있습니다. 즉 $\theta$가 최대가 되는 지점을 찾기 위해 $\theta$를 통해 편미분을 진행 하게 됩니다.

\[\begin{array}{l} \frac{d}{d \theta}\left(a_{H} \ln \theta+a_{T} \ln (1-\theta)\right)=0 \\ \frac{a_{H}}{\theta}-\frac{a_{T}}{1-\theta}=0 \\ \theta=\frac{a_{H}}{a_{T}+a_{H}} \end{array}\]

위을 결과를 살펴 보편 $\theta$는 $\frac{a_H}{a_{T}+a_{H}}$을 얻게 됩니다. 즉, 던저진 횟수 분해 앞면(H)가 나온 확률을 의미합니다. 이것은 우리가 이전의 예시에서 살펴 보았던 $\frac{앞면 수}{던진 횟 수}$와 같게 되는 것이지요. 이것은 MLE 관점에서 본 최적화된(=추정된) $\theta$라고 해석 할 수 있는 것이지요.


Simple Error Bound(오차 범위)

위에서 알아본 바에 따르면 θ̂ 에 영향을 미치는 것은 $αH$ 과 $αT$ 의 비율입니다. 전체 횟수인 n 이 커지더라도 이 비율만 지켜진다면 θ̂ 은 동일하게 됩니다.

동일한 비율을 가진 두 개의 데이터셋을 예로 들어봅시다. 한 데이터셋은 5번 던져 머리가 3번, 꼬리가 2번 나왔다고 합니다. 나머지 하나의 데이터셋은 50번 던져 머리가 30번, 꼬리가 20번 나온 경우입니다. 두 데이터셋 모두 최대 우도 추정을 통해 사건의 확률을 구하면 $\hat{\theta}=0.6=3 /(3+2)=30 /(30+20)$ 입니다. 그렇다면 두 데이터셋은 아무런 차이가 없는 것일까요? 데이터셋이 가지는 비율만 일정하다면 더 큰 데이터셋이 주는 이점은 없을까요?

질문에 대한 답은 “아니다” 입니다. 일단 우리가 지금까지 알아본 $\hat{\theta}$ 은 그저 추정값일뿐 실제 확률이 아닙니다. 추정값은 언제나 실제값과 오차가 있기 마련입니다. 오차는 둘 사이의 차이이므로 절댓값을 활용하여 $\vert \hat{\theta} - \theta^{*} \vert$의 의미는 진리의 모수를 의미)로 나타낼 수 있습니다. 수학자들은 이 오차에 수학적 기술을 적용하여 오차의 범위(Error bound) 를 구하는 식을 만들어 놓았습니다. 오차의 범위를 구하는 식은 아래와 같습니다.

\[\begin{aligned} P\left(\vert\hat{\theta}-\theta^{*}\vert \geq \epsilon\right) \leq 2 e^{-2 N \epsilon^{2}} \\ \because N=a_{H}+a_{T} \end{aligned}\]

위 식을 보면 오차가 임의의 작은 값 $\epsilon$ 보다 커질 확률은 $2 e^{-2 N \epsilon^{2}}$ 로 나타납니다. 즉, $\epsilon$ 이 동일한 조건에서는 실행횟수 $\boldsymbol{N}$ 이 증가할수록 오차의 범위가 줄어들게 된다는 의미입니다. 이러한 학습 방식을 팩 학습(Probably Approximate Correct learning, PAC learning)이라고 합니다. PAC learning의 목적은 높은 확률(Probably)로 낮은 오차 범위(Approximately Correct)를 갖도록 하는 것입니다. 즉 이를 달성하기 위해서는 데이터셋이 많아야 하고, 향후 머신러닝에서 커다란 데이터셋이 중요한 이유도 이 때문입니다.


최대 사후법(MAP)

기존의 최대 우도법의 개념에서 베이지안의 관점이 추가된 것이 바로 최대 사후법(MAP) 방법론이다. 앞선 예시예서 5번의 동전 던지기 시행에서 3번이 앞면이 나왔다. 그럼 확률은 $\frac{3}{5}$로 계산 된다. 하지만 우리가 알고 있는 동전 던지기의 확률은 $\frac{1}{2}$가 아닌가?

우리의 최대 관심사는 모수(parameter)이다. 즉, 내가 동전 던지기를 함으로써 얻을 수 있는 기댓값 분산을 알기 위해서 동전 던지기 본질의 확률이 궁금한 것이다.

이러한 모수(parameter)를 얻기 위해서 우기가 기존에 알고 있는 $\frac{1}{2}$이라는 확률에 우리가 추가로 관측한 확률인 $\frac{3}{5}$를 추가하여 모수를 계산할 수 있다는 관점이 바로 베이지안 관점이다. 즉, 기존의 불확실한 확률(동전 던지기 확률은 $\frac{1}{2}$이 아니야?)에 새로운 관측( $\frac{3}{5}$ )을 추가하여 기존의 정보를 갱신할 수 있는 방법론을 말하는 것이다.

이때 다음과 같이 베이즈 정리가 사용된다. 데이터가 존재 할 확룰($P(D)$) 분에 사전 정보가 존재할 확률($P(\theta)$) $\times$ 사전 정보가 주어졌을 때의 데이터의 확률 분포의 확률값(가능도, $P(D \mid \theta)$)를 통해 데이터가 주어졌을 때의 확률을 만들어 낼 수 있습니다.

\[P(\theta \mid D)=\frac{P(D \mid \theta) P(\theta)}{P(D)}\]

이전에 우리는 $P(D \mid \theta)$에 대해서 다음과 같이 정리하였습니다.

\[P(D \mid \theta)=\theta^{a_{H}}(1-\theta)^{a_{T}}\]

그리고, $\mathrm{P}(\theta)$의 사전확률을 구하기만 하면 우리는 사후확률을 얻을 수 있습니다.


베이지안 관점에서의 베이즈 정리

위에서 정리한 베이즈 정리는 다음과 같이 해석 될 수 있습니다. $P(D)$가 사라진 이유는 $D$라는 행위 자체가 이미 일어난 확률입니다. 이미 주어진 사실입니다. 즉, 정해진 사실이므로 정규화 상수(Normalize Constant)라고 합니다. 그러므로 $\theta$의 변화에 영향을 받기 않는 요소이기 때문에 무시 할 수 있는 것입니다. 요소 한개가 제거 되었기 때문에 더이상 등식을 사용할 수 없고 비례관계로 바뀌게 된 것입니다. \(P(\theta \mid D) \propto P(D \mid \theta) P(\theta)\)

위 식의 요소들은 우리가 이전에 구한 값들을 다음과 같이 사용하면 됩니다. 하지만, 사전확률 $P(\theta)$는 어떻게 정의 할 까요?

$P(D \mid \theta)$ 를 구할 때 우리는 이항분포를 사용해서 이를 구했습니다. 그것과 마찬가지로 $P(\theta)$ 를 구할 때도 다른 확률 분포를 사용해서 이를 구해야 합니다. 여러가지 확률 분포 중에서 베타 분포를 사용할 수 있습니다.

베타 분포는 다음과 같이 표현이 가능 합니다.

\[P(\theta)=\frac{\theta^{\alpha-1}(1-\theta)^{\beta-1}}{B(\alpha, \beta)}, B(\alpha, \beta)=\frac{\Gamma(\alpha) \Gamma(\beta)}{\Gamma(\alpha+\beta)}, \Gamma(\alpha)=(\alpha-1) !\]

이렇게 $P(\theta)$를 정의하기 위한 베타 분포의 파라미터는 $\alpha$와 $\beta$입니다. 이는 우리가 이항 분포에서도 사용된 파라미터와 비슷합니다. 이항 분포에서는 앞면이 나온 횟수와 뒷면이 나온 횟수를 사용헤서 $\theta$를 유도한 것과 같은 맥락 입니다.

이렇게 구한 가능도와 사전확률을 통해서 우리는 사후확률을 계산 할 수 있습니다.

\[\begin{array}{c} P(\theta \mid D) \propto P(D \mid \theta) P(\theta) \propto \theta^{a_{H}}(1-\theta)^{a_{T}} \theta^{\alpha-1}(1-\theta)^{\beta-1} \\ =\theta^{a_{H}+\alpha-1}(1-\theta)^{a_{T}+\beta-1} \end{array}\]

여기서, $B(\alpha, \beta)$를 사용하지 않은 이유는 베타분포에서 $\alpha, \beta$에 의해서 변하는 값 즉, $\theta$ 입장에서는 Constant 이므로 등식에서 제외하고 비례 관계로 사용 할 수 있습니다.


최대 우도법(MLE)과 최대 사후법(MAP)

최대 우도법(MLE)

우리는 이전에 최대우도법을 사용해서 다음과 같이 추정된 파라미터를 찾을 수 있었습니다.

\[\hat{\theta}=\operatorname{argmax}_{\theta} P(D \mid \theta)\]

이때의 각 요소는 다음과 같습니다.


최대 사후법(MAP)

여기서 최대 사후법은 모수와 데이터 분포를 바꾼 것에 지나지 않습니다. 즉, 가능도(likelihood)에 대해서 최대화 하는 것이 아닌, 사후확률(posterior)에 대해서 최대화 하는 것이지요.

\[\hat{\theta}=\operatorname{argmax}_{\theta} P(\theta \mid D)\]

위 식에서 $P(\theta \mid D)$는 다음과 같이 정의 됨을 확인 했습니다.

\[P(\theta \mid D) \propto \theta^{a_{H}+\alpha-1}(1-\theta)^{a_{T}+\beta-1}\]

이를 최대화하는 $\theta$를 찾으면 다음과 같습니다.

\[\hat{\theta}=\frac{a_{H}+\alpha-1}{a_{H}+\alpha+a_{T}+\beta-2}\]

최대 우도법과 최대 사후법에 대한 $\theta$를 최적화하는 방식은 같지만 관점이 다른 것입니다.

MLE에서는 사전 정보를 넣을 수 있는 방법이 없었지만, MAP를 활용하면 사전 확률을 통해 불확신한 확률을 갱신 할 수 있게 되는 것이죠.


결론

MLE와 MAP 수식을 살펴보면 $\theta$에 대한 추정값이 다소 다른 점들을 확인 할 수 있을 것입니다.

MLE

\[\hat{\theta}=\frac{a_{H}}{a_{H}+a_{T}}\]

MAP

\[\hat{\theta}=\frac{a_{H}+\alpha-1}{a_{H}+\alpha+a_{T}+\beta-2}\]

두 값은 다소 다르지만 실험을 많이 진행 할 경우 $a_H$의 값과 $a_T$의 값이 커지게 될 것이고 MAP 식의 $\alpha$와 $\beta$의 영향력이 작아짐에 따라 MLE 추정값과 같이 비슷해 질 것 입니다.

하지만, 실험 횟수가 부족하거나 데이터 수가 작은 경우 $\alpha, \beta$의 값은 아주 중요하게 작용 하게 될 것입니다. 즉, 관측값이 적은 경우에는 MLE오 MAP의 값은 아주 다르게 될 것입니다.


출처