[베이즈 통계학] 베이즈 정리의 두가지 맥락

베이즈 정리

베이즈 정리(Bayes’ theorem). 어떤 사건이 서로 배반하는 원인 둘에 의해 일어난다고 할 때 실제 사건이 일어났을 때 이것이 두 원인 중 하나일 확률을 구하는 정리를 베이즈의 정리라고 한다. 공식의 형태는 다음과 같습니다.

\[P(B \mid A)=\frac{P(A \mid B) P(B)}{P(A)}\]

베이즈 정리의 두 가지 맥락

역확률 문제

베이즈 정리는 원래 역확률(Inverse probability) 문제를 해결하기 위한 방법이였습니다. 즉, 조건부 확률 $P(B \mid A)$ 를 알고 있을때, 전제 사건의 관계가 정반대인 조건부 확률 $P(A \mid B)$ 을 구하는 방법이였습니다.

예를 들어, 병 A를 알고 있는지 판정하는 양성 판정 정확도(즉, 병A가 결린 사람이 실제로 테스트 결과 양성으로 나올 확률)가 90% 검사기가 있다고 가정해 봅시다. 이때, 어떤 사람이 이 검사기로 검사를 시행해서 양성 결과가 나왔다면, 이 사람이 90%의 확률로 병에 걸렸다고 이야기 할 수 있을까요? 그렇지 않습니다. 왜냐하면 검사가 알려주는 확률과 우리가 알고 싶은 확율은 조건부 확률의 의미에서 정반대이기 때문입니다.

• 검사의 양성판정 정확도 ‘90%는’ 검사가 병을 가진 사람을 정확하게 포착할 확률, 즉 병을 가지고 있다는 전제하에 검사 결과가 양성일 확률 90%를 의미합니다.
• 하지만, 우리가 알고 싶은 것은 검사결과가 양성이라는 전제하에 병을 앓고 있을 확률입니다. 조건부 확률의 관점에서 보면 전제(조건)의 관심 사건의 관계가 정반대이기 때문에, 이런 식의 확률을 구해야 하는 문제를 역확률 문제라고 합니다.

	전제	관심사건	수학적표현
검사의 정확도	병을 앓고 있다	검사 결과: 양성	P(검사 결과: 양성|병을 앓고 있다) = 0.90
우리의 관심사	검사 결과: 양성	병을 앓고 있다	P(병을 앓고 있다|검사 결과: 양성) = ….?

원래대로라면 검사의 정확도만을 가지고 우리의 관심사인 (양성인 사람이)병을 앓고 있을 확률을 알 수 없습니다. 하지만, 우리가 검사 대상인 질병의 유병률을 알고 있다면, 베이즈 정리를 통해 역확률을 계산 할 수 있습니다.

예를 들어, 전세계 인구중 1%의 사람들이 병 A를 앓는다고 알려져 있다고 가정 해 봅시다. 그리고 음성판정 정확도 (병 A가 걸리지 않는 사람이 실제로 테스트 결과 음성으로 나올 확률)도 양성판정 정확도와 마찬가지로 90%로 가정합시다. 그렇다면 검사 결과가 나온 사람이 실제로 A를 알고 있을 확률은 약 8.3%입니다.

\[\begin{aligned} P(\text { 병 } \mid \text { 양성 }) &=\frac{P(\text { 양성 } \mid \text { 병 }) P(\text { 병 })}{P(\text { 양성 })} \\ &=\frac{P(\text { 양성 } \mid \text { 병 }) P(\text { 병 })}{P(\text { 양성 } \mid \text { 병 }) P(\text { 병 })+P(\text { 양성 } \mid \text { 무병 }) P(\text { 무병 })} \\ &=\frac{0.9 \times 0.01}{0.9 \times 0.01+(1-0.9) \times 0.99} \approx 8.3 \% \end{aligned} \\ (\text{단, } P(B)=P(B \mid A) P(A)+P\left(B \mid A^{\subset}\right) P\left(A^{\subset}\right))\]

데이터를 이용한 사후 확률의 추정

이러한 베이즈 정리를 어떤 사건의 확률을 추론하는 알고리즘으로 관심을 가지는 사람들을 나이브 베이지안 알고리즘을 만든 사람들 입니다. 이 때는 어떤 사건이 일어날 확류에 대한 임의의 가정 $P(A)$에 실제로 발견된 자료나 증거 $B$를 반영해서, 자료로 미루어보아 어떤 사건이 일어날 확률 $P(A \mid B)$를 구하는 것이 관심이 대상이 됩니다.

앞의 진단검사 예제에서 문제를 ‘어떤 사람이 병 A에 걸렸을 확률을 계산하는 문제’로 조금 달리 접근해 봅시다.

1. 처음에는 어떤 사람이 병 A에 걸렸을 때 확률에 대해 아는 것이 없어, 전 세계 인구 절반이 해당 질병에 걸릴 확률인 1%의 유병률을 가정했다.
2. 그런데 정확도가 90%인 검사를 받았더닌 양성판정을 받았다.
3. 이 사람이 검사에서 양성판정을 받았다는 새로운 사실을 토대로 이 사람이 실제로 병에 걸렸을 확률을 알 수 있지 않을까?

이 문제에서 베이즈 정리가 알려주는 것은, 만약 우리가 ‘어떤 사건 A가 일어 났다고 가정할 때 B라는 자료를 얻게 될 확률' 에 대한 정보만 알고 있다면, 자료에 근거해서 어떤 사건이 일어날 확류을 새로 계산 할 수 있다는 것입니다. 위의 사례에서는 검사의 정확도가 ‘어떤 사건(병에 걸림)이 일어 낫다고 가정할 때 자료(양성 판정을 받음)을 얻게 될 확률‘에 대한 정보를 제공 해주기 때문에 이를 이용해 검사 결과를 토대로 그 사람이 병에 걸렸을 확률을 새로 계산 할 수 있습니다.

베이즈 정리 용어

이러한 관점에서 베이즈 정리를 접근 할 때는 다음과 같은 추가 용어가 등장 합니다.

\[\text{posterior} \propto \text{likelihood} \times \text{priror}\]

위 식을 정리하면 다음과 같습니다.

	(사건 A의) 사후 확률	$\propto$	가능도	$\times$	가능도
수학적 표현	P(A|B)	$\propto$	P(B|A)	$\times$	P(A)
예(진단검사)	P(병을 앓고 있다|양성 판정)	$\propto$	P(양성 판정|병을 앓고 있다)	$\times$	P(병을 앓고 있다)

• 사전확률(Prior) : 새로운 자료가 없는 상태에서 어떤 사건이 일어날 확률에 대한 가정이 필요한데 이를 사전 확률이라고 합니다.
• 가능도(Likelihood): 사건이 일어 났다는 가정하에 새로이 가지게 된 자료가 관측될 확률을 가능도라고 합니다.
• 사후 확률(posterior) : 사전확률과 가능도를 이용해서 새롭게 게산한, ‘(새로운 자료를 미루어 보아 새롭게 판단한) 어떤 사건이 일어날 확률’을 사후 확률이하고 합니다.

베이즈 정리의 분모에 해당하는 부분은 가능도(Likelihood)를 구할 대 조건으로 걸린사건 (위의 예시의 경우, (실제 병의 유무와는 상관없이)양성 판정이 나오는 확률)의 확률을 의미합니다.

기능적으로 사후 확률이 확률의 정의(0이상 1이하)를 충족 시키도록 사전확룰과 가능도의 곱을 보정해주는 역할을 합니다. 위의 같은 예에서는 식이 간단하여 계산이 쉽지만, 복잡한 경우 등식을 비례 관계로 바꾸어 생략 할 수 있습니다.

확률 vs. 가능도

확률 (Probability)

간단히 (전통적 관점에서) ‘확률’이란 주어진 확률분포가 있을 때, 관측값 혹은 관측 구간이 분포 안에서 얼마의 확률로 존재하는 가를 나타내는 값을 말합니다.. 여기서 중요한 것은 확률 분포(probability distribution)을 고정(fixed)하고 그 때의 관측 X 에 대한 확률을 구한다는 것! 이를 수식으로 표현하자면 아래와 같이 쓸 수 있습니다.

\[\text { 확률 }=\mathrm{P}(\text { 관측값 } \mathrm{X} \text { | 확률분포 } \mathrm{D} \text { ) }\]

예제

이를 그림으로 살펴보면 다음과 같습니다. 파란 확률 분포는 귀여운 쥐들의 몸무게 분포로써 평균 32 표준편다 2.5를 갖는 정규분포이다. 이때 해당 분포를 가정하고(고정하고) 쥐의 무게가 32-34 사이로 관측될 확률은 얼마 일까요? 이는 아래 그림의 빨간 영역(red area)이 이 확률을 말해줄 것입니다.

즉, 빨간 영역의 공간을 수식으로 정리하면 다음과 같습니다. $\mu= 23, \sigma=2.5$ 인 정규분포가 주어졌을 때의 쥐의 몸무게가 32와 34 사이일 확률을 구한 것이죠.

\(P(32 ≤ X ≤34 \mid N(32,2.5)) = 0.34\) 이는 다음과 같은 의미를 내포합니다. “사건의 범위는 변하지만, 분포는 고정되어 있다. “ 즉, 다음과 같은 수식을 정리가 가능 했던 것이지요. \(p(\text{data}\mid \text{distribution})\)

확률은 ‘어떤 고정된 분포‘에서 이것이 관측될 확률(Area under distribution)이다.

가능도(Likelihood)

위에서 설명한 전통적인 방식의 확률이 바로 우리가 중고등학교 때 배운 확률의 의미입니다. 고정된 확률분포에서 확률값을 구하는 것이였죠. 하지만 가능도(likelihood)의 의미는 약간 다른 의미로 사용됩니다.

‘가능도’란 어떤 값이 관측되었을 때, 이것이 어떤 확률 분포에서 왔을 지에 대한 확률입니다. 간단히 하면 확률의 확률이라고 할 수 도 있겠다. 이것을 수식으로 표현하자면 아래와 같습니다.

\[\text { 가능도 }=\mathrm{L}(\text { 확률분포D } \mid \text { 관측값X })\]

예제

쥐의 무게를 재어보니 몸무게가 34g이 나왔다. 이때 이 관측결과가 정규분포(m=32/sd=2.5)에서 나왔을 확률은 0.12(빨간 십자마크)이고 이것이 가능도입니다. 관측값이 고정되고, 그것이 주어졌을 때 해당 확률분포에서 나왔을 확률을 구하는 것입니다. 그렇다면 두번째 그림에서 평균을 34인 확률분포에서 나왔을 확률은 어떻게 될까요? 그림과 같이 그 가능도는 높아진 것을 확인할 수 있습니다.

위 예제를 수식을 표현하면 다음과 같습니다.

\[L(N(34, 2.5 \mid \text{쥐 몸무게=34})) = 0.13\]

이를 수식으로 정리하면 다음과 같습니다. 즉, 데이터가 주어졌을 확률 분포의 확률값을 구하는 것을 말합니다.

\[L(N(\mu, \sigma)\mid \text{data})\]

최대우도법 맛보기

위의 예제에서, 정규분포를 $\mu=33, \sigma=2.5$ 인 정규분포로 분포를 바꾸면 어떻게 될까요? 평균 값이 관측값에 가깝게 이동했으니 가능도의 값도 커지게 될 것입니다. MNIST 손글씨 예제를 떠올려 봅시다. 정답 레이블 분보가 다음과 같이 주어지고 신경망 모델 A, B, C를 통과 시켰을 때 다음과 같이 결과가 나온다고 가정 해봅시다.

정답레이블

모델 A, B, C

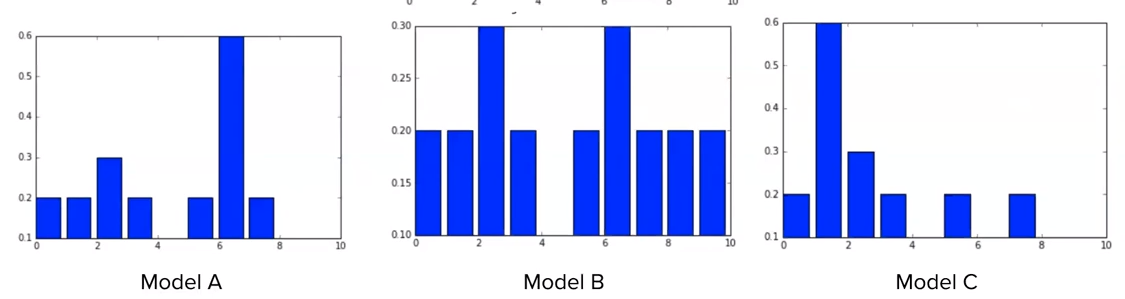
신경망 모델 A, B, C 중에서 정답 레이블의 분포와 가장 유사한 모델은 어떤 것 일까요? 바로 모델 C 입니다. 이전의 가능도의 정의를 상기 시켜 봅시다. $L(\text{distribution} \mid \text{data}) $ 즉, 데이터가 주어졌을 때 모델의 C의 가능도가 가장 높다고 이야기 할 수 있습니다. 우리가 딥러닝을 학습시켜 가능 과정은 이렇게 예측값의 데이터의 분포가 실제 데이터의 분포와 가장 유사한 분포를 찾은 것입니다.

조금 더 나아가서 우리는 분류 모델을 구현하고자 할 때 Cross-Entrophy를 이용을 했습니다. 그 이유가 위의 예시과 연관이 있습니다. Cross-Entrophy를 사용하면 분포와 분포간의 차이를 계산 할 수 있고 그 차이를 오차라고 하고 이 오차자가 작아지는 방향으로 학습을 진행하게 됩니다.

위의 내용을 포함하여 가능도를 정리하면 다음과 같습니다. 관측 데이터가 주어졌을 때, 그 데이터의 분포를 가장 잘 설명하는 분포에 높은 가능도 함수값을 주는 것입니다.

최대 우도법은 우리에게 주어진 데이터를 가장 잘 설명할 수 있는 예측 모델을 찾아거나 혹은 만들거가는 것이라고 생각하면 쉽습니다.

정리

기존의 역확률을 구하는 베이즈 정리의 사용에서 데이터를 이용한 사후 확률의 추정은 약간 다른 관점으로 접근 해야 합니다. 그 중요한 지점이 바로 신뢰도 라는 관점입니다. 역확률을 구할 때는 사용되지 않았던 사전확률, 가능도, 사후확률이아는 개념이 바로 이 신뢰도와 연관되어 생겨난 개념들 입니다.

즉, 결론 부터 말하자면 베이즈 정리는 새로운 정보를 토대로 어떤 사건이 발생했다는 주장에 대한 신뢰도를 갱신해 나가는 방법(a method to update belief on the basis of new information)입니다.

사건이 일어 났다는 가정하에 새로 가지게된 데이터가 관측될 확률(=가능도)와 어떤 사건이 일어날 확률에 대한 가정(=사전확률, 불확실성)을 통해 기존의 정보를 갱신해 불확실성을 개선 하는 것이지요.

빈도주의 관점 vs. 베이지안 관점

예를 들어 동전의 앞면이 나올 확률이 50%다 라는 주장이 있다고 가정 해봅시다.

• 빈도주의: 100번 동전을 던져쓸 때 50번은 앞면이 나온다
• 베이지안 주의: 동전의 앞면이 나왔다는 주장의 신뢰도가 50%이다

용어 정리

위에서 설명한 내용을 기반으로 베이즈 정리를 정리하면 다음과 같습니다.

\[P(H \mid E)=\frac{P(E \mid H) P(H)}{P(E)}\]

• H(Hypothesis) : 가설 혹은 ‘어떤 사건이 발생했다는 주장’

• E(Evidence): ‘새로운 정보’

• $P(H)$: 어떤 사건이 발생했다는 주장에 관한 신뢰도
• $P(H\mid E)$: 새로운 정보를 받은 후의 갱신된 신뢰도

이를 그림으로 정리하면 다음과 같습니다. 파란색 부분의 $P(H)$ 즉 사전확률(prior) 자체에 불확실성을 가지고 있기 때문에 이를 증거(Evidence) 즉, $P(E)$를 통해 어떻게 갱신 할 수 있는 지를 수식적으로 나타낸 것입니다.

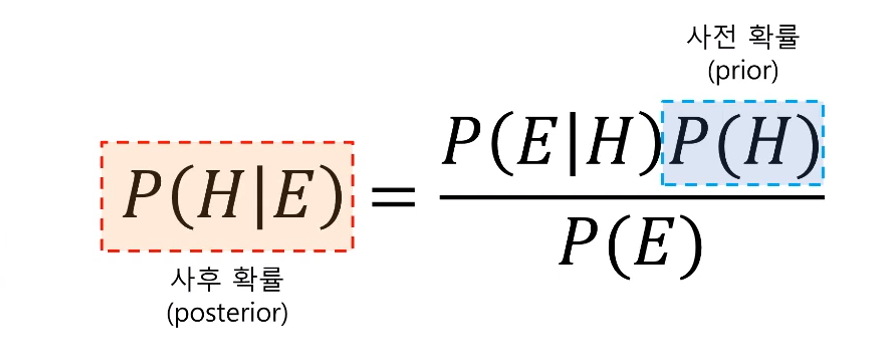
베이즈 정리의 의의

다시 한번 정리 하면, 베이즈 정리는 새로운 정보를 토대로 어떤 사건이 발생했다는 주장에 대한 신뢰도를 갱신해 나가는 방법(a method to update belief on the basis of new information)입니다.

기존의 통계학에서는 엄격하게 확률의 공간을 정의하거나 집단(모집단 혹은 표본집단)의 분포를 정의하고 그뒤에 계산을 통해 파생되는 결과물들을 수용하는 패러다임을 차용했습니다.

반면에, 베이지안 관점의 통계학에서는 사전확률과 같은 경험에 기반한 선험적인, 혹은 불확실성을 내포하는 수치를 기반으로 하고 거기에 추가적인 정보를 바탕으로 사전 확률을 갱신 합니다.

이러한 귀납적 추론 방식에서 베이지안 관점/통계학은 추가적인 근거를 확보를 통해 진리로 더 다가갈 수 있다는 철학을 내포하고 있는다는 점에서 빅데이터에서 사용되는 관점과 유사하다고 할 수 있습니다.

출처

• 베이즈 정리 - 위키백과, 우리 모두의 백과사전
• 베이즈 정리의 의미 - 공돌이의 수학정리노트