[PRML] 1장- 결정이론

Written by metterian
on 

들어가며

우리는 앞장에서 불확실성을 정량화시키고 일관된 수학적 프레임워크를 구성하는 과정을 살펴보았습니다. 이제 Decision 이론을 이용하여 확률 이론을 바탕으로 불확실성이 관여된 상황에서의 최적의 결정 과정을 살펴볼 것입니다.

목표 : 입력 x 와 이에 대한 타겟 t 를 이용하여 새로운 변수 $x_{new}$ 에 대응하는 타겟 값 $t_{new}$ 를 예측할 수 있다.


주의할 점

결정이론이란?

새로운 $\mathbf{x}$ 가 주어졌을때 확률모델 $p(\mathbf{x}, \mathbf{t})$에 기반해 최적의 결정(예: 분류)을 내리는 것을 말합니다.

\[p\left(C_{k} \mid \mathbf{x}\right)=\frac{p\left(\mathbf{x} \mid C_{k}\right) p\left(C_{k}\right)}{p(\mathbf{x})}\]

예제: X-Ray의 이미지로 암 판별

예를 들어 어떤 환자의 X-Ray 결과 $x$ 가 주어졌을 때 $t$ 는 환자의 암(cancer) 여부라 하자. 이 때 $t$의 값이 $C1$ 인 경우 암이고, $C2$ 인 경우 암이 아님을 의미합니다. 그래서 우리는 x-ray 이미지가 주어졌을 때 암의 여부를 분별하고 싶습니다. 이를 수식으로 나타내면 $p\left(C_{k} \mid \mathbf{x}\right)$ 으로 나타낼 수 있고 이를 정리하면 다음과 같습니다.

\[\begin{aligned} p\left(\mathcal{C}_{k} \mid \mathbf{x}\right) &=\frac{p\left(\mathbf{x}, \mathcal{C}_{k}\right)}{p(\mathbf{x})} \\ &=\frac{p\left(\mathbf{x}, \mathcal{C}_{k}\right)}{\sum_{k=1}^{2} p\left(\mathbf{x}, c_{k}\right)} \\ &=\frac{p\left(\mathbf{x} \mid \mathcal{C}_{k}\right) p\left(\mathcal{C}_{k}\right)}{p(\mathbf{x})} \\ & \propto \text { 우도(likelihood) } \times \text { 사전확률(prior) } \end{aligned}\]

우리의 목적은 잘못된 선택을 하게될 가능성을 줄이는 것입니다. (암이 아닌데 암이라고 선택, 암인데 암이 아니라고 선택) 따라서, 직관적으로 사후(posterior) 확률이 높은 클래스를 선택하는 문제로 귀결됩니다.


오분류 최소화 (Minimizing the misclassification rate)

앞서 언급했듯 우리의 목적은 어찌보면 잘못된 분류 가능성을 최대한 줄이는 것입니다. 따라서 모든 $x$ 에 대해서 특정 클래스로 할당시키는 규칙이 필요합니다. 이런 규칙은 결국 입력공간을 각 클래스 별로 나누는효과를 가지게 됩니다.

분류 오류 확률 (Probability of Misclassification)

클래스가 잘못 분류될 가능성을 생각해보면, 이것을 하나의 확률식으로 표현이 가능합니다.

\[\begin{aligned} p(\mathrm{mis}) &=p\left(x \in \mathcal{R}_{1}, C_{2}\right)+p\left(x \in \mathcal{R}_{2}, C_{1}\right) \\ &=\int_{\mathcal{R}_{1}} p\left(x, C_{2}\right) d x+\int_{\mathcal{R}_{2}} p\left(x, C_{1}\right) d x \end{aligned}\]

위 식은 $C_2$ 인데 $\mathcal{R}_1$로 분류될 확률 + $C_1$ 인데 $\mathcal{R}_2$로 분류될 확률을 합한 것입니다. 즉, 위 식이 나타내는 의미는 오분류될 확률 값을 모두 합한 확률로, 이를 최소화하는 조건을 세워 모델을 설계해야 합니다.

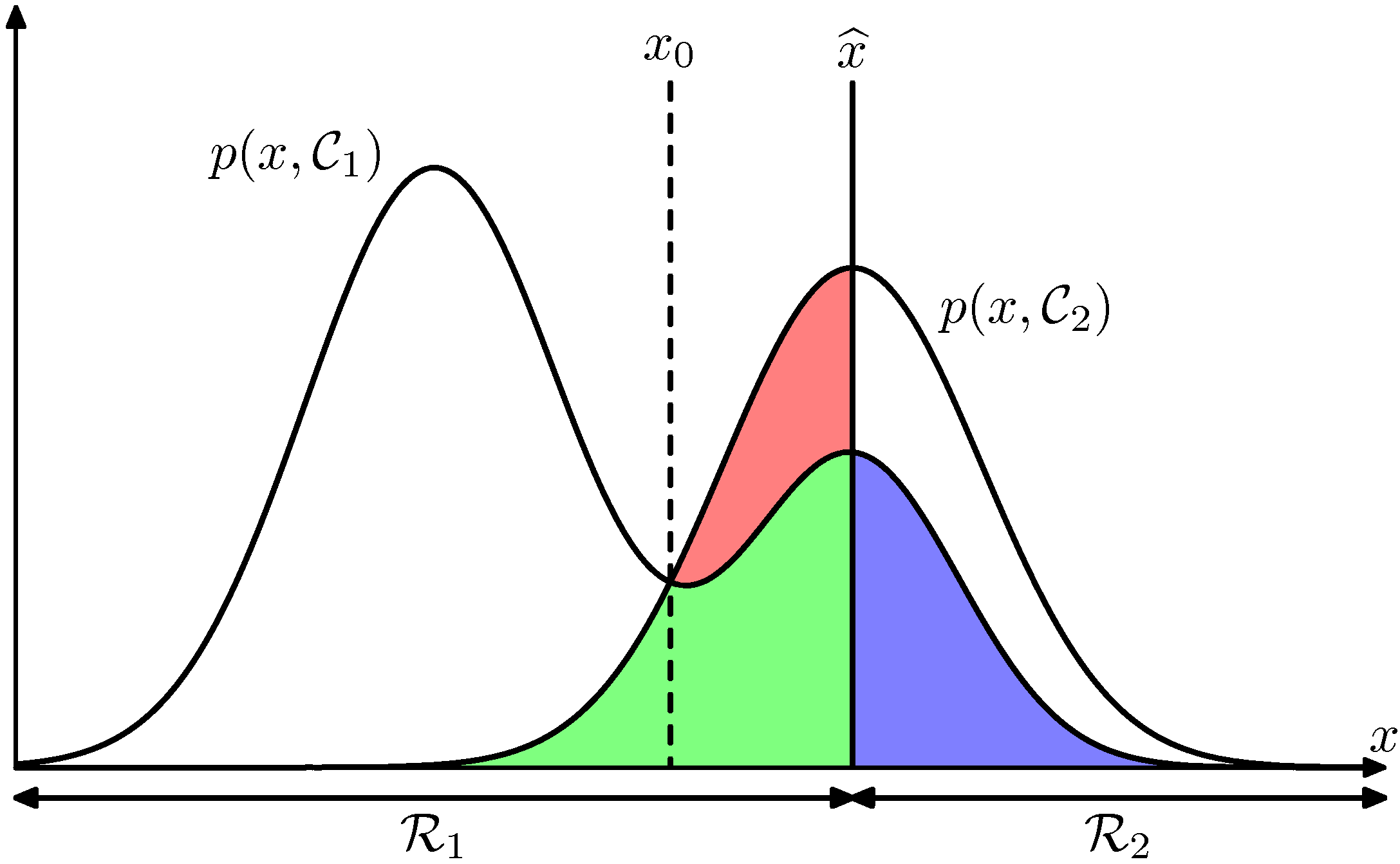
Figure1.24

위의 그림에서 현재 클래스의 구분선(decision boundary)를 $\hat{x}$ 라고 했다고 가정해봅시다. 그러면 $x \geq \widehat{x}$ 영역에서 해당 클래스가 $C_2$ 로 결정되어 집니다. (반대의 경우는 $C_1$ 으로 할당) 이를 색깔로 표현하면 오류의 합은은 파란색, 초록색, 빨강색이 됩니다. 이 색깔들의 영역을 최소화 하는 곳으로 decision boundary가 설정되어야 합니다.

만약 $\hat{x}$ 를 왼쪽으로 이동하면 초록색 + 파란색의 면적을 그대로 이지만, 빨강색의 영역은 작아지게 됩니다. 따라서 위 그림의 오류를 최소화 하는 방법은 $\hat{x}=x_{0}$ 지점까지 decision boundary를 이동 시킨는 방법 입니다.

앞서 설명한 수식과 같이 클래스가 오분류 될 가능성을 수식으로 표현 했지만 이는 반대로 제대로(올바르게) 분류될 확률값을 최대화 하는 형태로도 식을 표현해도 문제가 되지 않습니다. 이를 표현하면 다음과 같습니다.

\[\begin{aligned} p(\text { correct }) &=\sum_{k=1}^{K} p\left(\mathbf{x} \in \mathcal{R}_{k}, \mathcal{C}_{k}\right) \\ &=\sum_{k=1}^{K} \int_{\mathcal{R}_{k}} p\left(\mathbf{x}, \mathcal{C}_{k}\right) \mathrm{d} \mathbf{x} \end{aligned}\]


기대 손실 최소화 (Minimizing the expected loss)

앞서 설명한 내용에 오류가 있지는 않지만, 현실세계의 오분류(misclassification)을 설명하는데는 부족한 점이 있습니다.

예를 들어, 암(cancer)을 진단 하는 예제에서 오분류를 생각해 봅시다.

첫번째 경우보다 두번째 경우가 더 심각한 분류인데, 이렇게 오분류한경우 페털티를 강하게 주고 싶을 것입니다. 이러한 생각에서 나타는 것이 바로 손실 함수라는 개념입니다.


손실함수 (Loss Function)

단순히 오분류의 갯수를 구하는 것이 아니라, Loss라는 개념을 정의하고 이를 최소화 하는 방법을 생각해 봅시다. 이러한 방법을 통해 어떠한 결정에 대해 조금 더 능동적으로 행동을 조절 할 수 있게 됩니다. 개념은 간단합니다.

하나의 샘플 $x$가 실제로는 특정 클래스 $C_k$에 속하지만 우리가 이 샘플의 클래스를 $C_j$로 선택할 때(즉, 잘못된 선택을 한 경우, 오분류) 소요되는 비용을 정의합니다. 여기서 모든 경우에 대한 Loss 값을 정의한 행렬을 Loss 행렬이라고 합니다. 혹은 Loss를 Cost로 정의하기도 합니다.

수식

실제 Loss 함수를 최소화 하는 방법은 Loss 함수에 대한 평균값을 최소화 하는 방법을 사용합니다. 왜냐하면 솔실함수를 최소화하는 해가 최적의 해입니다. 하지만, 손실 함수값은 알려져 있지 않은 실제 클래스값을 알아야한 계산이 가능합니다. 주어진 입력벡터 $\mathbf{x}$에 대해서 실제 클래스 값에 대한 불확실성은 결합확률분포 $p(\mathbf{x}, \mathcal{C}_k)$로 표현됩니다. 그렇기 때문에 우리는 이 분포에 대해 계산한 평균 손실을 최소화하는 것을 목적함수로 설정할 수 있습니다.

\[E[L]=\sum_{k} \sum_{j} \int_{R_{j}} L_{k j} p\left(\mathbf{x}, C_{k}\right) d \mathbf{x}\]

위 식에서 $L_{k j}$ 잘못 분류 되었을 때의 페널티 값을 담고 있는 행렬입니다. 때문에 $j$ 로 잘못 분류된 값들을 모두 합하여 평균을 구하는 것이지요. 손실행렬의 예는 아래의 예제에서 확인 가능합니다.

위의 식 자체를 그냥 오류 함수로 정의 해서 사용하면 됩니다. (최소제곱법을 오류 함수로 사용한 것 처럼). 여기서 $x$ 는 반드시 어떤 $R_j$에 포함되게 됩니다. 따라서 우리는 오류값이 최소가 되는 $R_j$를 선택해야 합니다.

결론적으로, $x$에 대해 $\sum_{k} L_{k j} p\left(\mathbf{x}, C_{k}\right)$ 를 최소화 하는 클래스를 찾으면 됩니다. $p\left(\mathbf{x}, C_{k}\right)=p\left(C_{k} \mid \mathbf{x}\right) p(\mathbf{x})$ 로 치환이 가능하고. $p(\mathbf{x})$ 는 클래스마다 동일하다고 생각하고 생략합니다. 새로운 $x_{new}$가 들어왔을때, 이 식을 이용하면 됩니다.

\[\sum_{k}L_{kj}p(\mathcal{C}_k \mid \mathbf{x})\]

즉, 각각의 클래스에 대한 사후확률 $p(\mathcal{C_k}\mid\mathbf{x})$ 를 알고나면 이 방법을 쉽게 활용하여 계산 할 수 있습니다.


예제: 의료진단

다음과 같이 이진분류를 하는 클래스로 구분이 되어 있다고 가정해보자. $C_1$ 의 경우는 아픈 경우를 나타내고, $C_2$의 경우는 건간한 경우를 나타낸다.

\[\left.C_{k} \in\{1,2\} \Longleftrightarrow \text { sick, healthy }\right\}\]

이때, Loss 행렬은 다음과 같이 나타낼 수 있습니다. $L[0] = [0,100]$의 의미는 실제 sick을 의미하고, $L[1]=[1,0]$의 의미는 실제 heathly를 의미 합니다. 또한, 첫번째의 행의 의미는 sick이라고 분류한 경우를 나타내고 두번째 행의 경우는 health라고 분류한 경우를 나타냅니다.

\[L=\left[\begin{array}{cc} 0 & 100 \\ 1 & 0 \end{array}\right]\]

이때의, 기대손실을 구하면 다음과 같습니다. 즉 Loss 함수에 대한 평균값을 구하면 다음과 같습니다.

\[\begin{aligned} \mathbb{E}[L] &=\int_{\mathcal{R}_{2}} L_{1,2} p\left(\mathbf{x}, \mathcal{C}_{1}\right) \mathrm{d} \mathbf{x}+\int_{\mathcal{R}_{1}} L_{2,1} p\left(\mathbf{x}, \mathcal{C}_{2}\right) \mathrm{d} \mathbf{x} \\ &=\int_{\mathcal{R}_{2}} 100 \times\left(\mathbf{x}, \mathcal{C}_{1}\right) \mathrm{d} \mathbf{x}+\int_{\mathcal{R}_{1}} p\left(\mathbf{x}, \mathcal{C}_{2}\right) \mathrm{d} \mathbf{x} \end{aligned}\]


회귀를 위한 손실 함수 (Loss functions for regression)

위의 예제에서는 분류(classification)을 위한 결정이론을 살펴보았습니다. 이번에는 회귀(regression)문제에서의 손실함수를 다뤄 봅시다. 회귀문제의 결정단계에서는 각각의 $\mathbf{x}$ 에 대해서 $t$의 추정값 $y(x)$ 를 선택해야 합니다.


기대손실함수 (expected loss function)

회귀문제의 결정단계에서는 각각의 $\mathbf{x}$ 에 대해서 $t$ 의 추정값 $y(x)$ 를 선택 한다고 했을 때, 이 과정에서 손실 $L(t, y(x))$ 가 발생한다고 가정해 봅시다. 그러면 평균(기대) 손실은 다음과 같이 주어집니다.

회귀문제에서의 기대 손실함수(expected loss function)을 정의 해보면 다음과 같습니다.

\[E[L]=\iint L(t, y(\mathbf{x})) p(\mathbf{x}, t) d \mathbf{x} d t\]

회귀 문제에서 일반적으로 손실힘수로서 사용하는 것은 $L\left(t_{y}(\mathbf{x})\right)={y(\mathbf{x})-t}^{2}$ 로 주어지는 제곱 손실입니다. 이 때 기대 손실은 다음과 같습니다.

\(E[L]=\iint\{y(\mathbf{x})-t\}^{2} p(\mathbf{x}, t) d \mathbf{x} d t\) 우리의 목표는 $E[L]$ 를 최소화하는 $y(x)$ 를 찾는 것입니다. 위 식을 미분하면 다음과 같이 나타낼 수 있습니다. 즉, 기대 손실 함수를 에러 함수로 놓았다고 생각하면 쉽습니다.

\[\frac{\delta E[L]}{\delta y(\mathbf{x})}=2 \int\{y(\mathbf{x})-t\} p(\mathbf{x}, t) d t=0\\ y(\mathbf{x})=\frac{\int t p(\mathbf{x}, t) d t}{p(\mathbf{x})}=\int t p(t \mid \mathbf{x}) d t=E_{t}[t \mid \mathbf{x}]\]

위 식은 $\mathbf{x}$ 가 주어졌을 때 $t$ 의 조건부 평균으로써 회귀 함수(regression function)이라고 합니다. 이에 대한 그림이 다음과 같습니다.

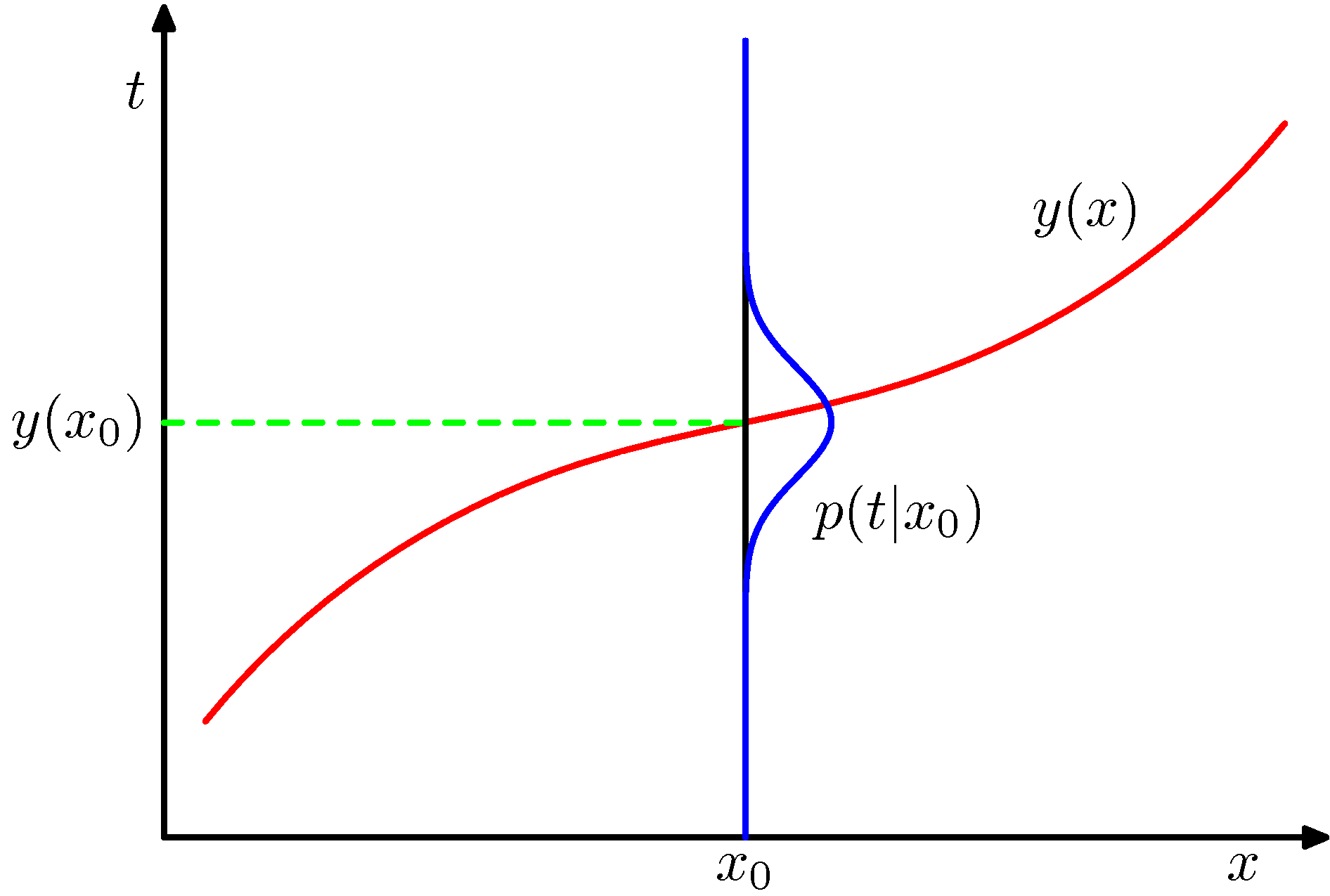
Figure1.28

위의 그림은 tt 가 1차원의 데이터이지만 NN 차원 벡터로 출력되는 것도 가능하다. 이 경우 $y(\mathbf{x})=E_{t}[\mathbf{t} \mid \mathbf{x}]$가 될 것입니다.

위 식을 결과들은 약간 다른 방식을 통해서도 도출해 낼 수 있습니다.

\[\begin{array}{c} \{y(\mathbf{x})-t\}^{2}=\{y(\mathbf{x})-E[t \mid \mathbf{x}]+E[t \mid \mathbf{x}]-t\}^{2} \\ =\{y(\mathbf{x})-E[t \mid \mathbf{x}]\}^{2}+2\{y(\mathbf{x})-E[t \mid \mathbf{x}]\}\{E[t \mid \mathbf{x}]-t\}+\{E[t \mid \mathbf{x}]-t\}^{2} \end{array}\]

최초의 식에다가 $E[t \mid \mathbf{x}]$ 값을 더하고 빼고 해서 식을 확장했습니다. 여기서 수식은 다음과 같습니다.

즉, 존재 가능한 모든 경우의 데이터를 확보해 평균값을 구하면 실제의 최적 함수를 만들 수 있습니다. 하지만, 실질적으로 이는 불가능합니다. 때문에 샘플 데이터를 통해서만 예측 값을 추정해야 하는 것입니다.

만약, 샘플 데이터로 부터 추정된 $y(\mathbf{x})$ 의 값이 $E[t \mid \mathbf{x}]$ 값(실제 정답)과 동일하다면 매우 휼륭한 식으로 추정된 것입니다. 위의 식을 정리하면 다음과 같습니다

\[E[L]=\int\{y(\mathbf{x})-E[t \mid \mathbf{x}]\}^{2} p(\mathbf{x}) d \mathbf{x}+\int \operatorname{var}[t \mid \mathbf{x}] p(\mathbf{x}) d \mathbf{x}\]

위 식에서 $y(\mathbf{x})$ 과 $E[t \mid \mathbf{x}]$ 이 동일하다면 즉, 예측 값(근사한 값)과 실제 정답의 평균이 같다면 두 번째의 행의 값만 남게 됩니다. 사실 우리는 평균 손실 즉, 오류를 최소화 하는 방향으로 식을 근사하기 원하므로 $y(\mathbf{x})$ 과 $E[t \mid \mathbf{x}]$ 이 최대한 동일하게 만들고 싶을 것입니다.

하지만, 여기서는 에러 를 구성하는 요소를 파악하기위해 이런 식을 뜯어 보고 있는 것입니다. 위의 수식대로 기대 손실(expected loss)은 크게 2가지 요소로 나누어 볼 수 있습니다. 첫번째 행은 실제 값과 예측 값의 차이를 의미하고, 두번째 행은 분산으로써 샘플이 포함하고 있는 노이즈(noise)를 의미합니다.

결론

앞서 살펴 본 분류 방식에서도 최적의 결정을 내리기 위한 방법들을 살펴보았는데, 마찬가지로 회귀(regression)와 관련된 문제들도 이런 접근법을 생각해 볼 수 있습니다.