[PRML] 1장 - 확률이론

Written by metterian
on 

핵심 개념

다항식 곡선 근사 (Polynomial Curve Fiting)

다음과 같은 곡선을 중심으로 데이터를 예측하는 모델을 구현하고자 한다

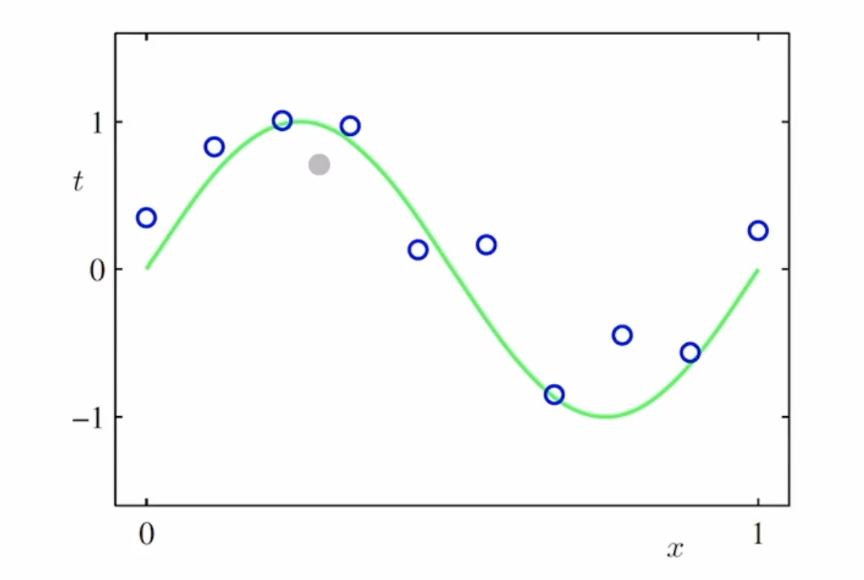
image-20210602141937868

문제 정의


함수의 근사

이러한 다항식 곡선 문제를 풀기 위해서는 각 데이터를 근사 할 수 있는 적절한 함수를 찾는 것이 중요합니다. 다음 식과 같이 다항식 함수를 사용하여 이를 근사하는 모델을 구성 할 수 있습니다.

\[y(x, \mathbf{w})=w_{0}+w_{1} x+w_{2} x^{2}+\ldots+w_{M} x^{M}=\sum_{j=0}^{M} w_{j} x^{j}\]

얼핏보면 위 식은 $x$ 에 대해서 다항식의 형태를 띄고 있습니다. 그렇지만 모델의 파라미터($W$)에 관해서는 선형식(linear)입니다. 이렇게 모델의 입력이 무엇이고 가중치가 무엇인지 구분하는 것이 중요합니다. 여기 가중치($W$)는 고정되어 있고 입력에 대해서 $x$ 가 계속 변하는 것입니다. 우리는 이러한 입력에 대해서 고정된 가중치를 찾아 내는 것이 목표 입니다.


오차 함수(Error Function)

image-20210602143614023

이렇게 모델이 주어져있고 입력이 주어져 있으면 가중치를 찾아야 합니다. 어떻게 찾을 것인가 하는 방법론 중에서는 오차함수를 사용하는 것 입니다. 오차 함수란 입력 값의 데이터와 모델의 값의 차이를 함수 형태로 표현한 것을 나타냅니다. 일반적으로 오차 함수의 가장 대표적인 표현 방법은 제곱합(sum of square)입니다.

\[E(\mathbf{w})=\frac{1}{2} \sum_{n=1}^{N}\left\{y\left(x_{n}, \mathbf{w}\right)-t_{n}\right\}^{2}\]

추가적으로, 위 식은 가중치 $W$ 에 대해서 이차식 형태를 띄고 있습니다. 때문에 가중치 $W$에 대해서 미분을 통해 최소값을 구할 수 있습니다.


과소적합(Under-fiting)과 과대적합(Over-fiting)

image-20210602143818546

추가적으로, 우리가 구하고자 하는 다음의 식에서 $M$ 의 값을 결정 해줘야 합니다. $M$ 의 값은 가중치의 갯수와 입력 데이터의 차원을 결정하게 됩니다. 여기서 $M$ 의 값을 결정하는 것을 바로 모델 결정(Model Selection)이라고 불리우는 중요한 과정을 나타냅니다.

\[y(x, \mathbf{w})=w_{0}+w_{1} x+w_{2} x^{2}+\ldots+w_{M} x^{M}=\sum_{j=0}^{M} w_{j} x^{j}\]

데이터의 차원이 커질 수록 입력 데이터에 대해 정확도가 올라가지만, 새로운 데이터에 대해서는 과도한 차원 수로 인해 예측력이 감소 할 수 밖에 없습니다.


과대적합 여부 판단

위의 예시 처럼 평면상에 데이터를 표현 할 수 있을 때는 과대적합 여부를 쉽게 이해하교 확인 할 수 있지만, 고차원의 데이터의 경우 이를 파악하기가 어렵습니다. 이를 해결하기 위해 오류(Error)를 측정하여 과대 적합 유무를 확인 할 수 있습니다. 다항식 곡선근사에서는 $E_{RMS}$ 스코어를 사용하여 이를 판단 합니다.

\[E_{\mathrm{RMS}}=\sqrt{2 E\left(\mathbf{w}^{\star}\right) / N}\]

$N$으로 나눔으로써 데이터 사이즈가 다른 경우에도 비교할 수 있도록 하였고, 제곱근을 취함으로써 $E_{RMS}$가 target값 $t$와 같은 크기를 가지도록 하였습니다.

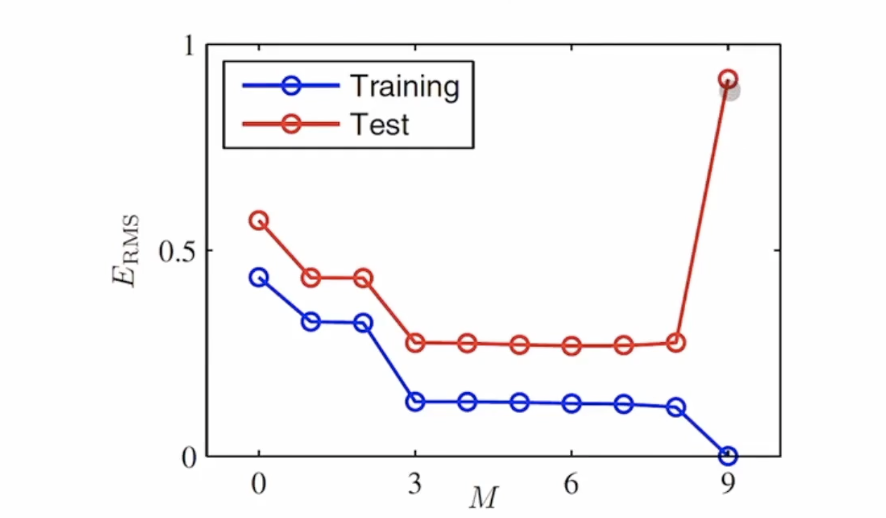
image-20210602151350047

위 그림을 살펴 보면 $M$ 이 9일 때, 훈련 데이터와 Testing 데이터의 오류의 차이가 심하게 나기 시작합니다. 즉, 훈련데이터에 심하게 과대적합되서 검증데이터에서 결과치가 낮게 나타는 현상입니다. 이렇게 오류 스코어를 통해서 과대적합의 유무를 판단 할 수 있습니다.


과대적함의 Pitfall

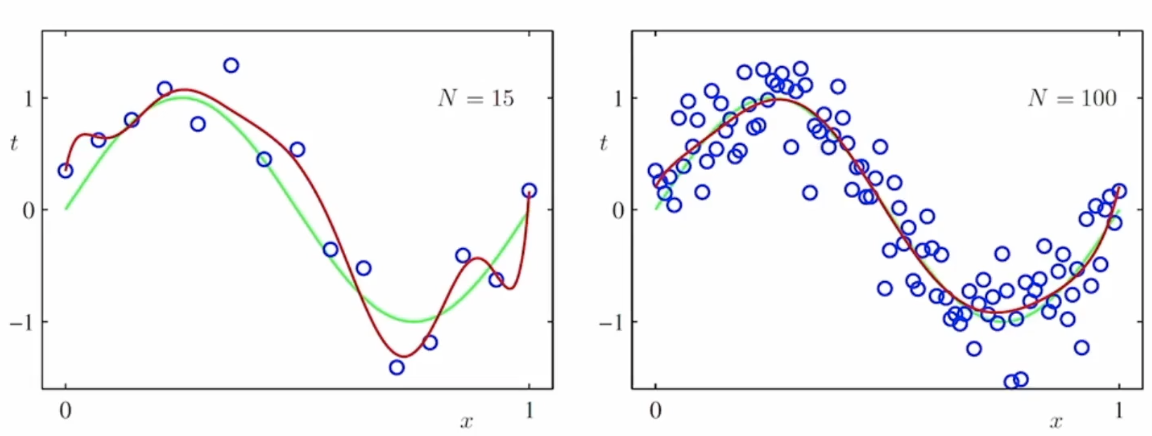
차원 수를 높여서 과대적합을 이르키는 것이 무조건적으로 안 좋은 것일 까요? 꼭 그렇지만은 않습니다. 다음 그림과 같이 $M=9$ 일 때, 데이터 수 $N$ 을 늘려보면 다음과 같습니다. 데이터 수가 늘어 남에 따라 과적합된 모델일지라도 원래의 함수의 모형을 잘 근사하는 모습입니다. 즉, 데이터가 많아 질 수록 좀 더 복잡한(=차원 수가 더 큰)모델을 사용해도 된다는 것 입니다.

M = 9

image-20210602151912855


규제화 (Regularization)

다음 그림은 $M$의 값으 변화에 따라 가중치(계수)들이 어떻게 변화 하는지를 나타낸 표입니다. 여기서 눈여겨 봐야 할 것은 $M$ 이 커질 수록 가중치의 값도 커진다는 점입니다. 모델이 복잡해 질 수록 이러한 현상을 보정하기 위해 가중치의 절대값 자체가 커지게 되는 것 입니다.

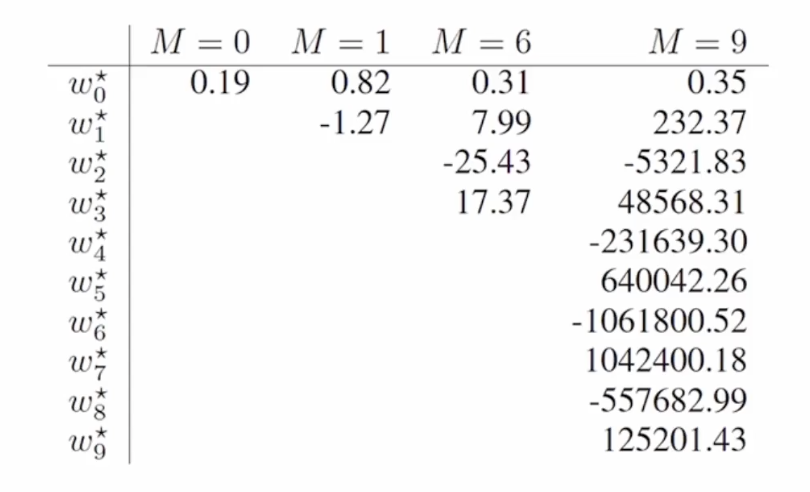
image-20210602152227817

이렇게 가중치가 커지면 너무 커지지 않게 가중치(계수)를 제한하면 좋지 않을까? 라는 생각을 하게 됩니다. 이를 규제화라는 방식을 사용해서 이를 구현 할 수 있습니다. 즉, 값이 너무 커지지 않게 식에 값을 제한 할 수있는 장치를 삽입하는 것입니다.

다음 식과 같이, 가중치에 대해 $L2 Norm$을 구한 값에 $\frac{\lambda}{2}$를 스칼라배 해주어 규제화를 하게 됩니다. 즉, $\lambda$ 값을 통해서 가중치를 크게 할 것인지 규제를 할 것인지를 선택할 수 있게 됩니다.

\[\begin{array}{l} \tilde{E}(\mathbf{w})=\frac{1}{2} \sum_{n=1}^{N}\left\{y\left(x_{n}, \mathbf{w}\right)-t_{n}\right\}^{2}+\frac{\lambda}{2}\|\mathbf{w}\|^{2} \\ \\\text { where }\|\mathbf{w}\|^{2} \equiv \mathbf{w}^{\mathrm{T}} \mathbf{w}=w_{0}^{2}+w_{1}^{2}+\ldots+w_{M}^{2} \end{array}\]

위 식의 표현은 다음 그림과 같이 나타낼 수 있습니다. $\lambda$ 값이 작아질 수록 규제화의 강도 낮게 되어 우리가 이전에 구한 식과 비슷하게 되고, $\lambda$ 값이 커지게 되면 규제화의 강도가 커지게 되어 차원의 수가 작아지게 됩니다(=모델의 복잡성이 낮아지게 됩니다. )

image-20210602153004438

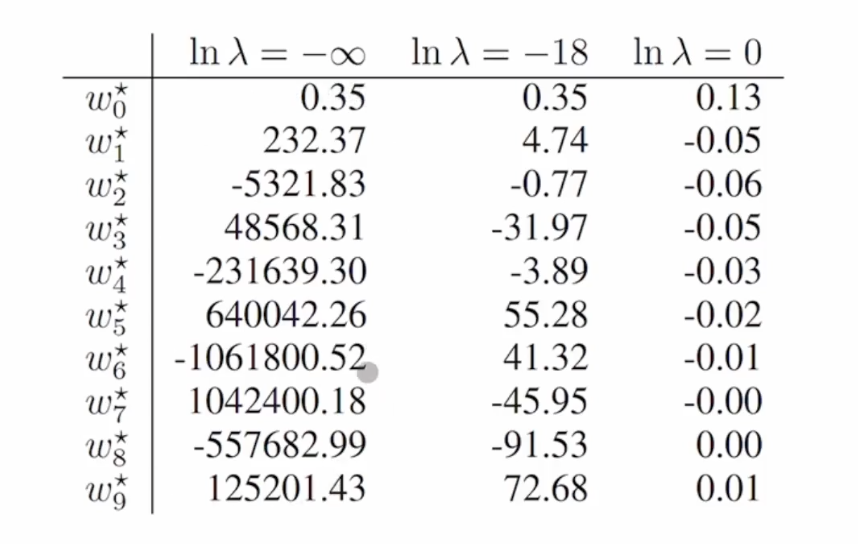
$M=9$ 일 때 가중치 값들

$M=9$ 일때의 각 계수를 구하면 다음과 같습니다. $\lambda$ 가 커질수록 규제화의 강도가 커져, 가중치의 값들이 작아지는 모습을 살펴 확인 할 수 있습니다. ``

image-20210602153413589

1.2.4 가우시안 분포

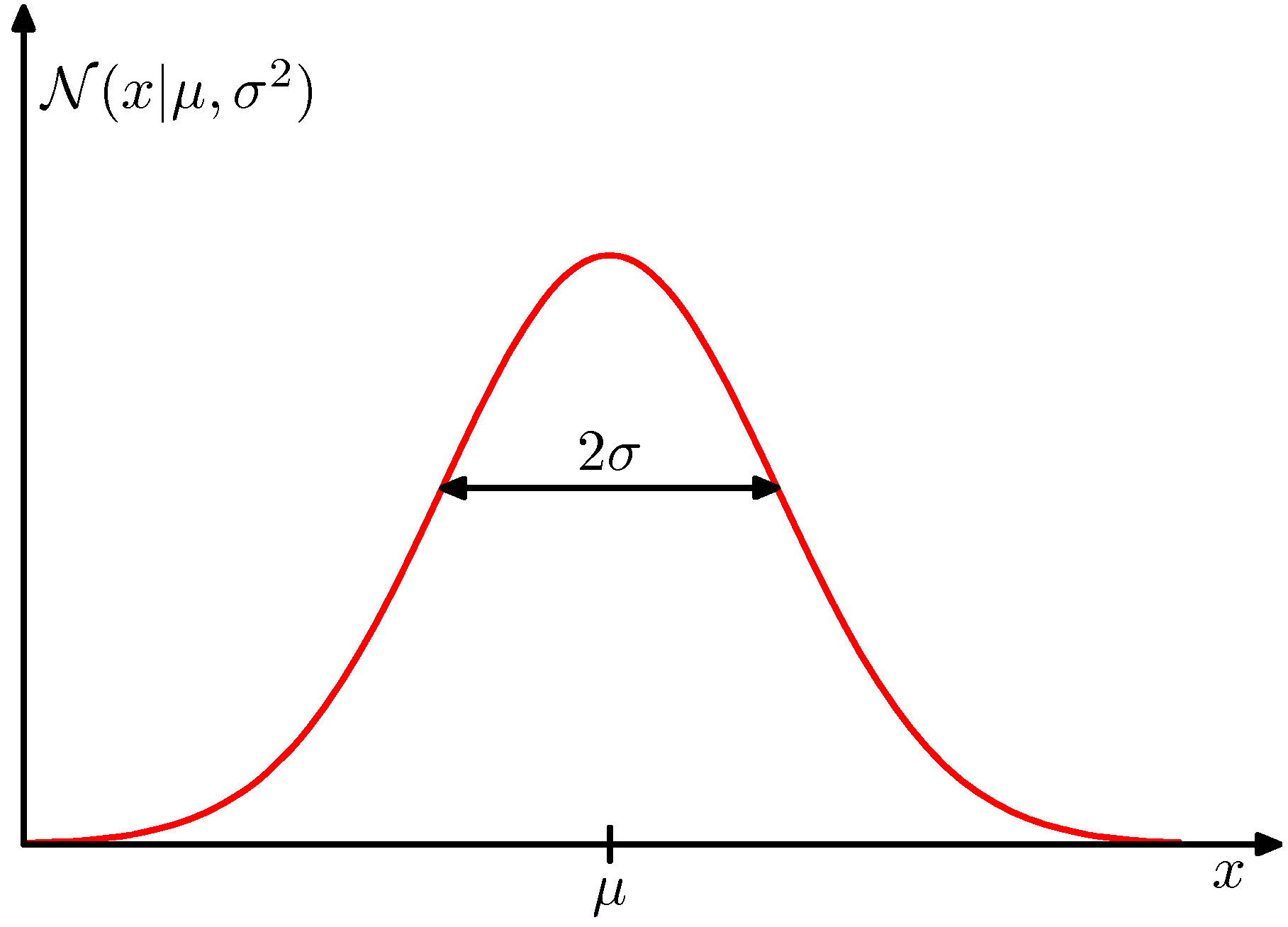
단일 변수 $x$ 에 대해서 가우시안 분포는 다음과 같이 정의 됩니다.

\[N\left(x \mid \mu, \sigma^{2}\right)=\frac{1}{\left(2 \pi \sigma^{2}\right)^{1 / 2}} \exp \left\{-\frac{1}{2 \sigma^{2}}(x-\mu)^{2}\right\}\]

위 식에서 두개의 파라미터(매개변수) $\mu$ 와 $\sigma^2$ 에 의해서 통제(control) 됩니다.

정확도(Precision)

또한 분산의 역수 $\beta=1 / \sigma^{2}$ 를 정확도(precision)이라고 정의합니다. 분산의 역수를 정확도를 계산하는데는 다음과 같은 이유가 있습니다.

정규 분포

Figure1.13

가우시안 분포를 정규분포라고 부르고, 이 분포는 다음과 같은 성질이 있습니다.

\[N\left(x \mid \mu, \sigma^{2}\right)>0\\ \int_{-\infty}^{\infty} N\left(x \mid \mu, \sigma^{2}\right) d x=1\\ E[x]=\int_{-\infty}^{\infty} N\left(x \mid \mu, \sigma^{2}\right) \cdot x d x=\mu\\ E\left[x^{2}\right]=\int_{-\infty}^{\infty} N\left(x \mid \mu, \sigma^{2}\right) \cdot x^{2} d x=\mu^{2}+\sigma^{2}\\ \operatorname{var}[x]=E\left[x^{2}\right]-E[x]^{2}=\sigma^{2}\]

다변량 정규 분포

위에서 설명한 것은 $x$가 1차원(단변량)인 경우이고, 이를 $D$ 차원으로 확장이 가능 합니다. (이것이 바로 가우시안 분포의 가장 큰 장점입니다.) 이를 다변량(multinomial) 가우시안 분포라고 부릅니다.

\[N(\mathbf{x} \mid \boldsymbol{\mu}, \mathbf{\Sigma})=\frac{1}{(2 \pi)^{D / 2}|\mathbf{\Sigma}|^{1 / 2}} \exp \left\{-\frac{1}{2}(\mathbf{x}-\boldsymbol{\mu})^{T} \mathbf{\Sigma}^{-1}(\mathbf{x}-\boldsymbol{\mu})\right\}\]

다변량 정규분포는 평균 벡터 $\mu$ 와 공분산 행렬 $\sum$ 이라는 두개의 매개변수에 의해 통제 됩니다. 위 식에서 각 기호의 의미는 다음과 같습니다.

다변수 정규분포에서 공분산 행렬은 양(+)의 대칭 행렬이여야 한다. 따라서, 역행렬이 항상 존재합니다. 공분산의 역행렬은 $\Sigma^{-1}$ 로 표현하고 정밀도 행렬(precision matrix)라고 합니다.


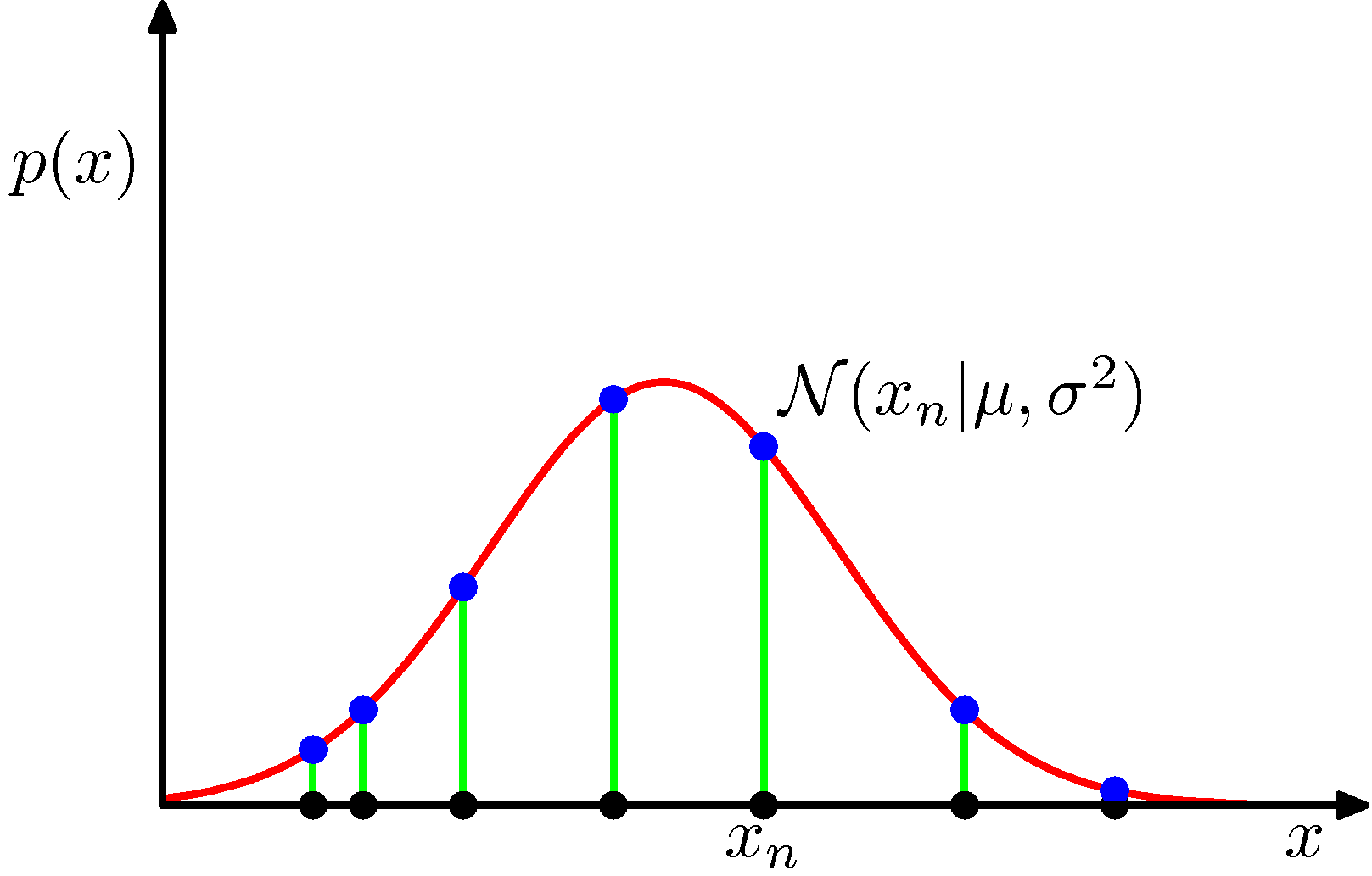
하나의 관측 데이터 집합(스칼라로 이루어진 벡터) $\mathbf{x}=\left(x_{1}, \ldots, x_{N}\right)^{T}$ 이 주어졌다고 가정해 봅시다. 이는 관측된 $N$ 개의 스칼라 변수 $x$ 를 지칭합니다. 여기서 벡터값을 가지는 변수의 한 관측값 $(x_1, \dots, x_D)^T$ 과 구별하기 위해서 $\mathbf{x}$ 를 사용하였습니다. 매개변수($\mu, \sigma$)를 가지는 가우시안 분포에서 관측값들을 독립적으로 추출 한다고 가정합니다.

이때 데이터 집합(벡터)하나가 관찰될 확률은 어떻게 알까요? (이전에는 $x$ 한개의 값을 추정하는 것이 였다면, 지금 부터는 $x$ 가 여려개인 집합의 값을 추정 하는 것 입니다.)

각각의 데이터가 발현되는 가능성은 서로 독립적(즉, i.i.d)이 확률 값들은 모두 독립 사건으로 처리할 수 있습니다. (확률의 곱으로 표현 가능)

하나의 데이터는 동일한 분포로 부터 발현 되었을 것이므로 이므로 이 확률을 다음과 같이 표기 할 수 있고 이를 가능도 함수라고 표기 합니다.

\[p\left(\mathbf{x} \mid \mu, \sigma^{2}\right)=\prod_{n=1}^{N} N\left(x_{n} \mid \mu, \sigma^{2}\right)\]

이를 그림으로 표현 하면 다음과 같습니다.

Figure1.14

그럼 어떤 관측 데이터가 하나의 가우시안 분포를 따른 다고 생각해 봅시다. 우리가 얻는 것은 관측 데이터 집합이고 이를 이용하여 원래의 가우시안 분포를 결정하는 문제가 보통 우리에게 주어진 문제 입니다.

쉽게 말하자면, 주어진 샘플이 어떻게 생겨먹은 가우시안 분포(=어떤 매개변수를 지니고 있는 가우시안 분포: 분포의 모양을 알면 확률값을 추정 가능)에서 나왔는지를 추정하는 것입니다. 이 경우 해를 구하는 것은 특정 가우시안 분포의 평균과 분산을 찾기만 하면 됩니다.

어떤 평균값을 갖는 확률밀도(확뷸분포, 여기서는 가우시안 분포)로 부터 이 샘플들이 추출되었을까?

즉, 이제 우리는 $ p\left(\mathbf{x} \mid \mu, \sigma^{2}\right)$ 가능도 함수를 이용하여 이러한 관찰 결과를 만들어 낼 만하다고 생각 할 수 있는 가장 타당한 $\mu$ 와 $\sigma$ 를 찾기만 하면 됩니다. 이를 파라미터 추정이라고 부릅니다. 주어진 데이터를 이용하여 선택한 모델에 대한 파라미터(모수)를 결정하는 문제입니다. 데이터의 모수를 알면 확률분포의 모양을 알 수 있고, 확률 분포의 모양을 알면 앞으로의 확률 값을 예측 할 수 있게 때문지요

여기서는 가능도 함수 $p\left(\mathbf{x} \mid \mu, \sigma^{2}\right)$ 를 구하기 위해 $log$ 를 사용하여 식을 전개 합니다.

\[\ln p\left(\mathbf{x} \mid \mu, \sigma^{2}\right)=-\frac{1}{2 \sigma^{2}} \sum_{n=1}^{N}\left(x_{n}-\mu\right)^{2}-\frac{N}{2} \ln \sigma^{2}-\frac{N}{2} \ln (2 \pi)\]

최대 우도법(MLE)

이 가능도 함수에서 각 매개변수를 최대로 하는 최적점을 찾으면 매개변수의 추정값을 구할 수 있습니다. 예를 들어 $\mu$ 의 추정값을 구하기 위해 가능도 함수를 $\partial\mu$로 편미분을 해주면 됩니다. 이렇게 구한 매개변수 추정값은 다음과 같습니다.

\[\mu_{M L}=\frac{1}{N} \sum_{n=1}^{N} x_{n}\\ \sigma_{M L}^{2}=\frac{1}{N} \sum_{n=1}\left(x_{n}-\mu_{M L}\right)^{2}\]

가능도 함수를 가장 크게 만드는 매겨변수를 추정한다는 의미로 이를 최대우도법(MLE)이라고 합니다. 이를 간단히 ML이라고도 표기하는 경우도 많습니다.

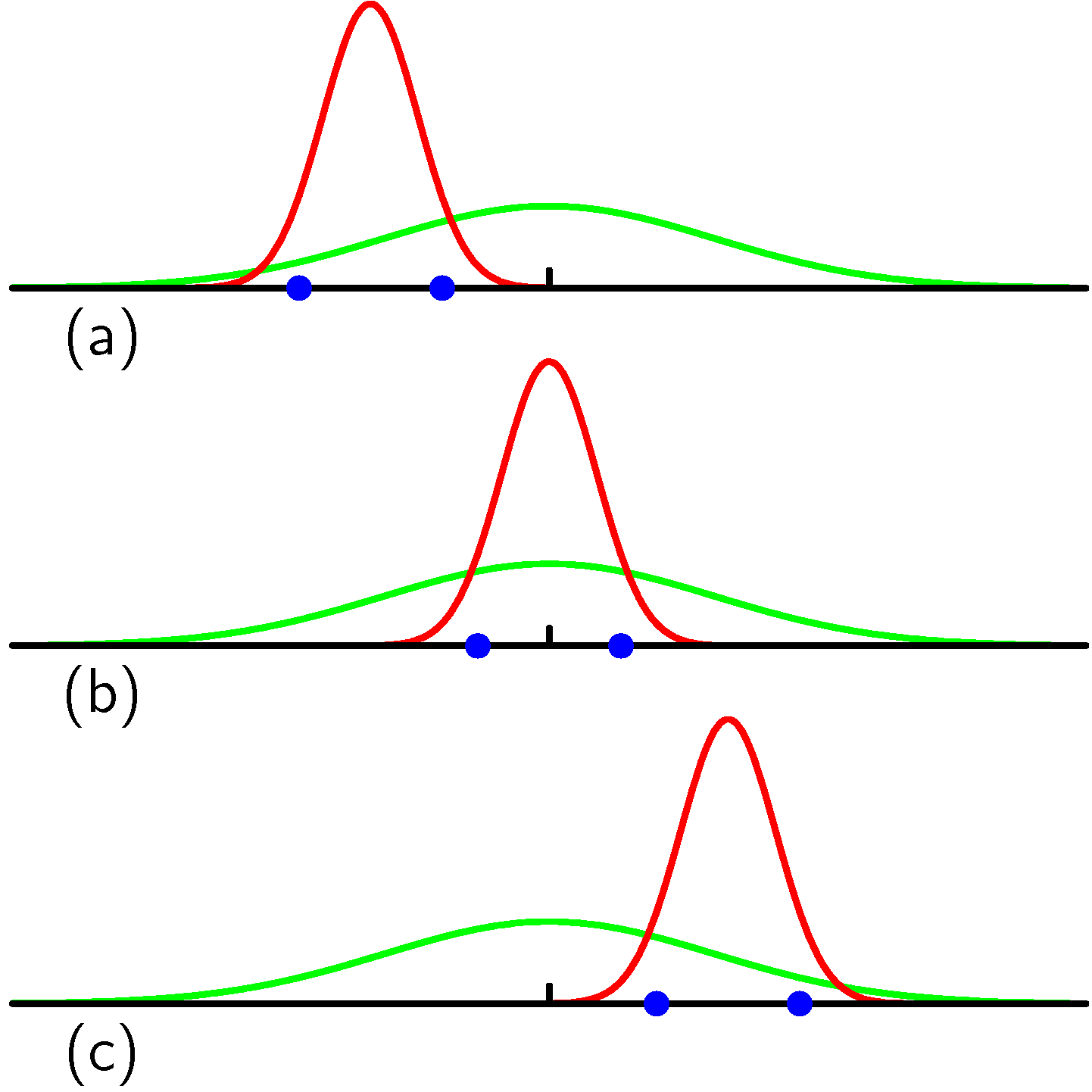
분산의 편향

사실, 위의 결과에서 분산 값은 편향(bias) 되어 있습니다. MLE에서 보여지는 오버피팅의 한 예인 것이지요. 이 값들의 평균값은 다음과 같습니다. 다음과 같이 평균의 평균을 구하게 되면 올바르게 모수의 평균을 구할 수 잇습니다.

\(E\left[\mu_{M L}\right]=\mu\) 하지만 분산의 경우는 모수의 분산과 차이(bias된)가 발생합니다. 분산의 평균값은 다음과 같습니다. 분산의 평균은 모수의 분산보다 $\left(\frac{N-1}{N}\right)$ 만 큼 작게 예측되어집니다.

\(E\left[\sigma_{M L}^{2}\right]=\left(\frac{N-1}{N}\right) \sigma^{2}\) 위 식으로부터 얻어진 아래의 분산 값은 unbias 되어 있음 을 알 수 있습니다.

\[\tilde{\sigma}^{2}=\frac{N}{N-1} \sigma_{M L}^{2}=\frac{1}{N-1} \sum_{n=1}^{N}\left(x_{n}-\mu_{M L}\right)^{2}\]

다음 그림은 매개변수의 bias, unbias를 이해하고지 제시된 그림입니다. 3개의 샘플 집합에 대해 각각의 평균 값을 평균하면 실제 평균 값에 가까워 집니다.(녹색이 실제 모집단의 정규 분포). 하지만, 분산의 경우에는 세개 집합의 분산 값을 평균해보아도 실제 분산값에 가까워지지 않습니다. 이것이 바로 bias, unbias에 대한 내용입니다.

모수 추정집합의 평균값이 실제 모수값과 같아지면 unbias, 실제 모수값과 차이가 나면 이를 bias라고 합니다

Figure1.15


1.2.5 곡선 피팅

곡선 피팅의 문제의 목표는 $N$개의 입력값 $\mathbf{x} = (x_1, \dots, x_N)^2$ 과 해당 타겟값 $\mathbf{t} = (t_1, \dots, n_N)^T$가 주어진 상황에서 새로운 입력변수 $x$가 주어졌을 때 그에 대한 타깃 변수 $t$ 를 예측해 내는 것을 말합니다. 이때 확률 분포를 이용하여 타겟변수의 값에 대한 불확실성을 표현 할 수 있습니다. 이를 위해, 주어진 $x$ 값에 대한 $t$ 값이 $y(x, \mathbf{w})$ 를 평균으로 가지는 가우시안 분포를 가진다로 가정 할 것입니다.

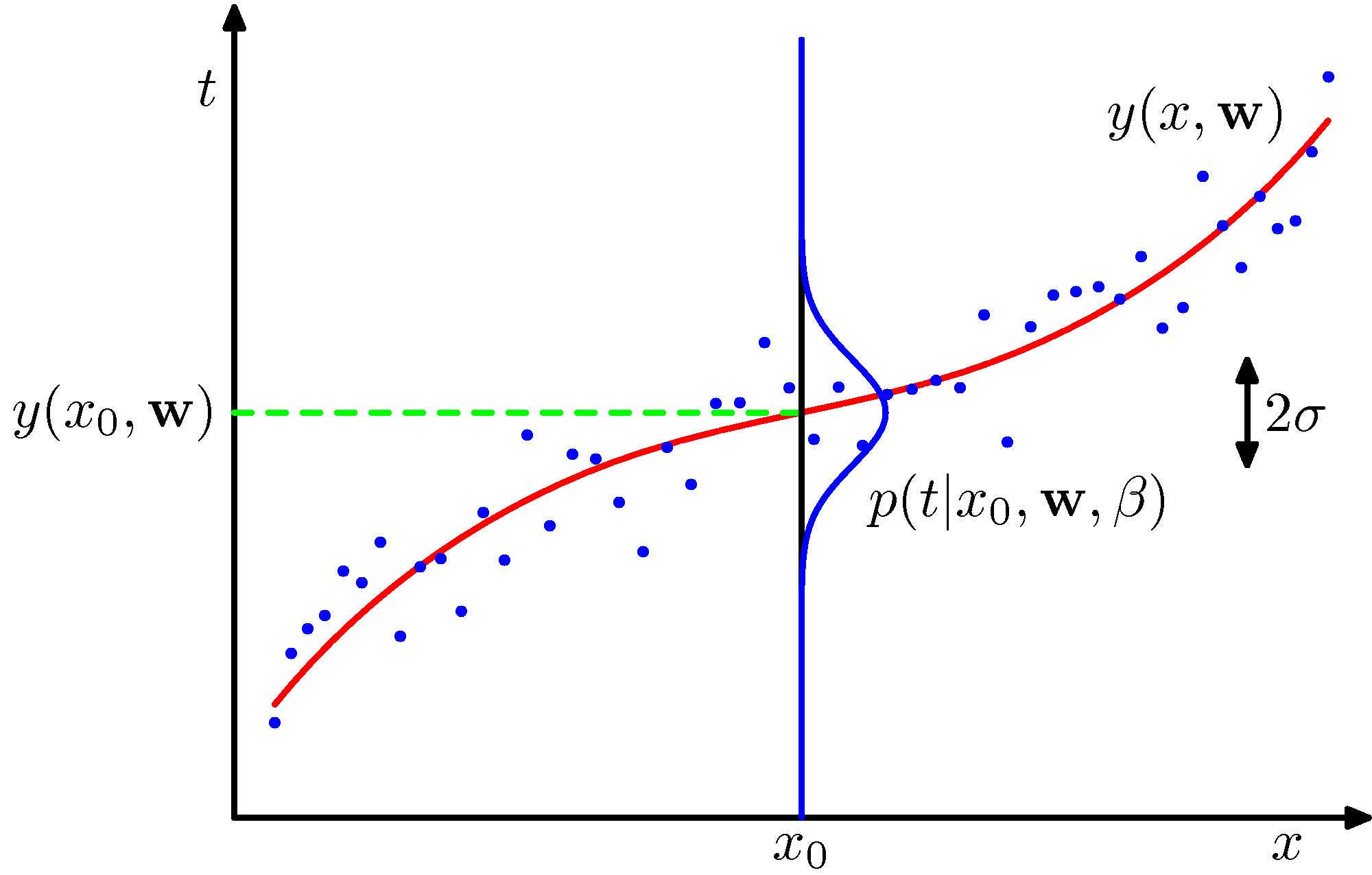
Figure1.16

주어진 환경을 다음과 같이 모델링할 수 있습니다.(그림 참고). 앞절에서 다루던 모델과는 약간 다르게 보일 것인데, 노이즈를 가우시안 분포로 고려하고 있습니다.

식의 차이를 잘 살펴보도록 하자. ( 식에 사용된 β 를 눈여겨 봐야 한다.) \(p(t \mid x, \mathbf{w}, \beta)=N\left(t \mid y(x, \mathbf{w}), \beta^{-1}\right)\)

여기서 β는 노이즈의 정확도(precision)로써 실제 분포의 분산 값의 역수입니다. 위 식을 풀이 하자면 주어진 매개변수($x, \mathbf{w}, \beta$)를 추정하기 위해 주어진 데이터를 이용하여 각 매개변수를 추정하는 것을 목표로 앞니다. 각 매개변수를 추정하면 노이즈에 대한 확률 분포를 얻을 수 있기 때문입니다.

즉, 한 점이 주어질 때 이를 나타낼 수 있는 근사식(가중치가 고려된 예측 모델)과 정규분포 형태의 노이즈 함수를 조합한 형태의 모델입니다. 따라서, 근사식(예측모델)을 현재 축의 중심에 두고 정규분포 형태를 가지는 노이즈 함수를 도입한것입니다.

가능도 함수의 사용

위 내용을 기반으로 가능도 함수를 정의 하면 다음과 같습니다. 실제 얻어진 샘플(관측데이터)의 결과와 이에 영향을 미치는 모수들의 관계를 확률식으로 표현 합니다.

\[p(\mathbf{t} \mid \mathbf{x}, \mathbf{w}, \beta)=\prod_{n=1}^{N} N\left(t_{n} \mid y\left(x_{n}, \mathbf{w}\right), \beta^{-1}\right)\]

위 가능도 함수에 로그를 취하고 함수값을 최대로 만드는 매개변수 값을 추정합니다.

\[\ln p(\mathbf{t} \mid \mathbf{x}, \mathbf{w}, \beta)=-\frac{\beta}{2}\left\{y\left(x_{n}, \mathbf{w}\right)-t_{n}\right\}^{2}+\frac{N}{2} \ln \beta-\frac{N}{2} \ln (2 \pi)\]

위 식으로 부터 얻어지는 $\mathbf{w}$ 의 최적점은 $\mathbf{w}_{ML}$이라고 표기합니다. 위 식에서 $\beta=1$ 이라고 생각하면 기존의 에러 함수와 차이가 없다는 것을 알 수 있습니다. 결국 sum-of-squares error function 인 것이지요.

다시 MLE를 이용하여 $\beta$ 값도 얻을 수 있습니다.

\[\frac{1}{\beta}=\frac{1}{N} \sum_{n=1}^{N}\left\{y\left(x_{n}, \mathbf{w}_{M L}\right)-t_{n}\right\}^{2}\]

타깃값 예측

이렇게 얻어진 $\mathbf{w}$ 와 $\beta$ 값을 이용하여 새로운 데이터 $x_{n e w}$ 의 타겟 값을 예측해 볼 수도 있습니다. 이전의 예측값은 하나의 점을 추정 하였지만, 이제는 예측 값이 존재할 확률 분포로 표현이 가능 합니다. 이러한 확률 모델을 predictive 분포라고 부릅니다.

\[p\left(t_{\text {new }} \mid x_{\text {new }}, \mathbf{w}_{M L}, \beta_{M L}\right)=N\left(t_{\text {new }} \mid y\left(x_{\text {new }}, \mathbf{w}_{M L}\right), \beta_{M L}^{-1}\right)\]

매개변수에 대한 확률분포

사실 여기서 베이지언 관점으로 식을 확장하여 파라미터 자체에 대한 확률 분포를 추가로 고려해볼 수도 있습니다. 즉, 사용되는 파라미터가 하나의 고정된 값이 아니라 랜덤 변수라고 가정하는 것입니다.

\[p(\mathbf{w} \mid \alpha)=N\left(\mathbf{w} \mid 0, \alpha^{-1} \mathbf{I}\right)=\left(\frac{\alpha}{2 \pi}\right)^{(M+1) / 2} \exp \left\{-\frac{\alpha}{2} \mathbf{w}^{T} \mathbf{w}\right\}\]

$M+1$ 은 벡터 $\mathbf{w}$ 의 개수로 다항식 예제에서는 최대 $M^{t h}$ 의 차수를 가지는 다항식이 만들어집니다. 여기서 $\alpha$ 와 같은 변수를 초모수(hyper-parameter)즉, 하이퍼 파라미터라고 부릅니다.

위 식에 가우시안 분포를 이용해 전개를 하면 다음과 같은 식을 얻을 수 있습니다.

\[\frac{\beta}{2} \sum_{n=1}^{N}\left\{y\left(x_{n}, \mathbf{w}-t_{n}\right)\right\}^{2}+\frac{\alpha}{2} \mathbf{w}^{T} \mathbf{w}\]

결국 위 식도 앞서 다루었던 정규화된 오류 함수(regularized sum-of-squares error function)와 식이 동일 합니다. 위식에서 $\lambda$ 만 $\lambda = \alpha/\beta$ 로 치원 하면 됩니다. 이 부분이 어렵게 느껴진다면 베이지언 방식을 통해서 정규화와 동일한 효과를 가지는 식이 유도 됨을 기억 하면 됩니다.


베이지안 곡선 피팅

들어가며

앞선 예제에서 $p(\mathbf{w} \mid \alpha)$ 에 대해 논의 했습니다. 이것을 베이지안 방식이라고 합니다. 완전한 베이지안 (fully bayseian) 접근법에서는 실제 가능한 모든 $\mathbf{w}$ 에 대한 값을 반영해야 합니다. 즉, $\mathbf{w}$ 를 고정된 값이 아니라, 확률 변수(확룰 분포로 해석될 수 있게)로 고려되어야 합니다. 따라서, 주변(marginaliztion) 확률 분포를 통해 베이지안 방식을 도입하여 $\mathbf{w}$ 에 대한 값을 확률 값을 구할 수 있습니다.

매개변수(parameter)에서는 모든 가능한 범위를 확률함수(확률분포)로 표현 할 수 있습니다. 즉, 모수가 어떤 확률 분포를 따른다고 가정하고(매개변수도 확률변수이기 때문에) 모수에 대한 확률값을 구할 수 있습니다. 여기서 모수의 모수값을 초모수(hyper-paprameter)라고 합니다.

모수의 모수도 확률변수이기 때문에 값이 변할 수 있지만, 여기서는 초모수인 $\alpha$ 와 $\beta$ 를 알여지지 않은 고정된 값으로 취급하여 모델을 전개 합니다. 초모수는 MLE에서 모수 역할을 생각하면 쉽습니다. MLE에서 데이터 샘플을 사용해서 모수를 추정할때처럼 초모수를 추정하기 위해 모수를 사용하여 MLE를 이용하는 것입니다.

주어진 문제

기존 곡선 피팅문제에서는 관측데이터 $\mathbf{x}$ 와 타켓 데이터 $\mathbf{t}$ 벡터를 이용하여 모델을 구성하고 새로운 데이터 $x$ 에 대해 $t$ 를 예측하는 방식을 취했습니다.

그러나, 베이지안 방식에서는 기존의 데이터를 새로운 데이터를 예측하는 모델을 하나의 수식으로 정리가 가능합니다.

\[p(t \mid x, \mathbf{x}, \mathbf{t})=\int p(t \mid x, \mathbf{w}) p(\mathbf{w} \mid \mathbf{x}, \mathbf{t}) d \mathbf{w}\]

이를 예측 분포(predictive distribution)이라고 부릅니다. 기존의 관측한 샘플데이터는 벡터 $(\mathbf{x}, \mathbf{t})$ 라고 표기하고 예측할 데이터는 $(x, t)$ 라고 표기합니다.

이러한 방식의 장점은 특정한 $\mathbf{w}$ 값을 고정하는 것이 아니라 $\mathbf{w}$에 대한 모든 가능성이 확률 분포로 표현되는 것이 장점입니다(불확실성을 표현 가능). 즉, 불확실한 사전확률(샘플 데이터, 가중치 분포)을 확률을 갱신하는 방법을 통해 더 사후확률(예측값)을 표현 하는 것입니다.

$p(\mathbf{w} \mid \mathbf{x}, \mathbf{t})$ 을 사전확률 분포이고 이를 정규화 하여 다음과 같은 식을 얻을 수 있습니다.

\[p(t \mid x, \mathbf{x}, \mathbf{t})=N\left(t \mid m(x), s^{2}(x)\right)\]

이 때 평균과 분산은 다음과 같습니다.

\[m(x)=\beta \phi(x)^{T} \mathbf{S} \sum_{n=1}^{N} \phi\left(x_{n}\right) t_{n}\\\]

위 식을 통해 예축 분포의 평균과 분산이 $x$ 에 종속되어 있음을 알수 있습니다. (평균과 분산이 $x$ 에 의해 통제 된다.)

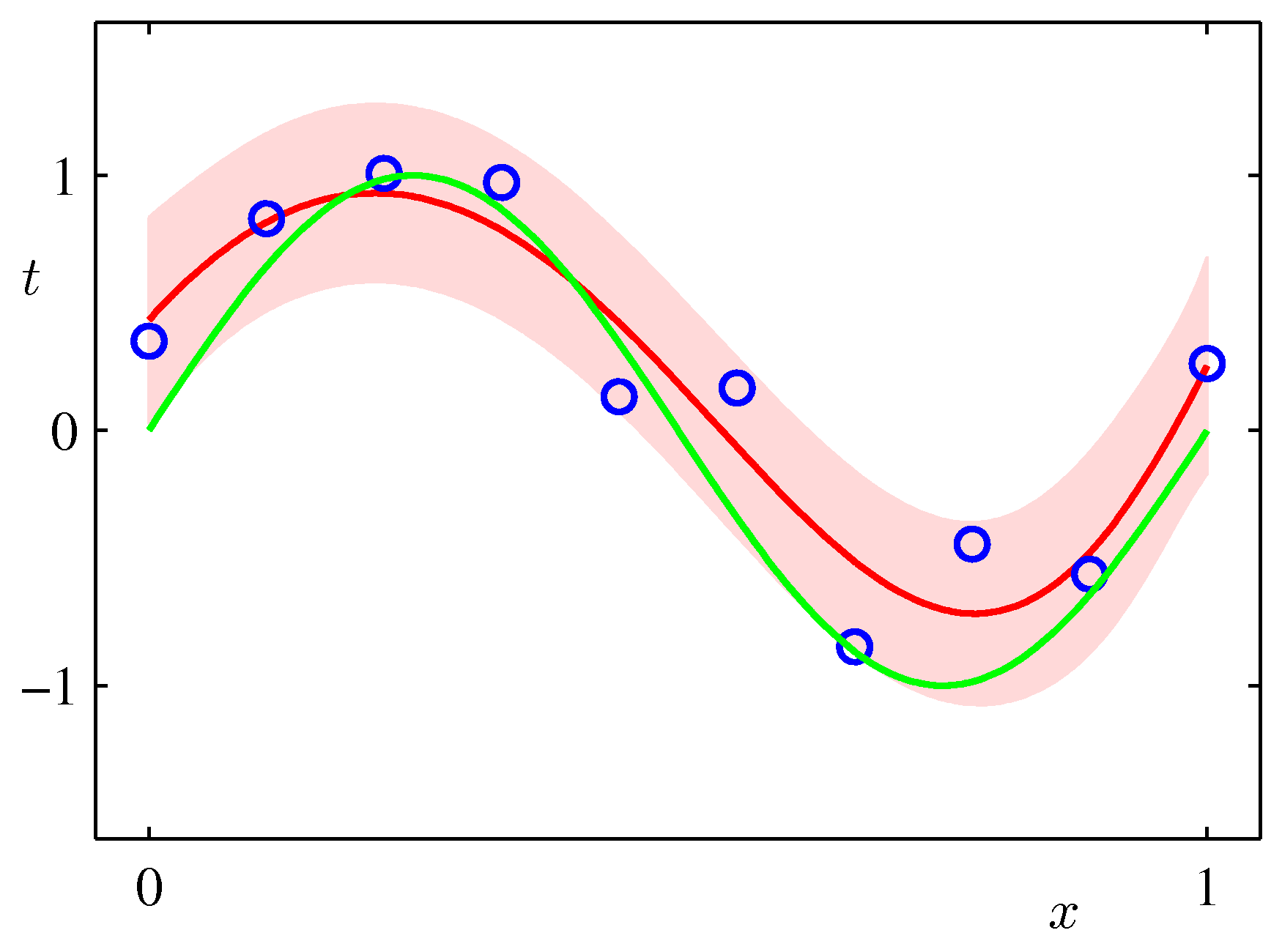
Figure1.17