[PRML] 2장 - 확률분포

밀도 추정(Density Estimattion)

밀도 추정 : $N$ 개의 관찰 데이터(observations) $\mathbf{x}{1}, \ldots \mathbf{x}{N}$ 가 주어졌을 때 분포함수 $p(\mathbf{x})$ 를 찾는 것을 말합니다.

분포함수(확률분포)를 구할 수 있으면 모든 문제를 찾을 수 있습니다. 회귀문제, 분류문제 등 확률 분포를 통해 결합분포를 유도해 낼 수 있기 때문입니다. 밀도 추정을 하기 위해서는 다음과 같은 과정 혹은 전재조건이 필요합니다.

1. $p(\mathbf{x})$ 를 파라미터(매개변수)화(parametric) 된 분포로 가정한다. 분류문제에서는 주로 $p(t \mid \mathbf{x}), p(\mathcal{C} \mid \mathbf{x})$ 를 추정한다.

   매개변수화 된 분포라고 불리는 이유는 이분포들이 몇개의 파라미터를 통해 확률 분포가 결정되기 때문입니다. 이말은 즉슨, 매개변수에 의해 확률분포가 변한다는 의미이고 즉, 매개변수를 찾기만 하면 확률분포를 찾을 수 있다는 말입니다.

2. 분포의 매개변수를 찾는다.

   1. 빈도주의 방법(Frequentist’s way): 어떤 기준(ex: 가능도)를 최적화 시키는 과정(최대우도법)을 통해 매개변수를 찾습니다.
   2. 베이지언 방법(Bayesian way): 먼저 파라미터의 사전확률(prior distribution)을 가정하고 베이즈 정리를 통해 매개변수의 사후확률(posterior distribution)을 구합니다.

3. 매개변수를 찾았다면(한 개의 값이든 분포든) 그것을 사용해서 “예측”을 할 수 있습니다.

켤레사전분포(conjugate prior): 사후확률이 사전확률(분포)와 동일한 분포를 갖도록 해주는 것입니다.

켤러사전분포를 사용해서 사전확률과 사후확률의 분포가 같아지게 되면 계산이 용이하여 사용하는 것입니다.

이항변수(Binary Variables) : 빈도주의 방법

이항 확률변수(binary random variable)인 $x$가 $x \in{0,1}$ 인 상황 (ex: 동전던지기)가 다음을 만족한다고 가정해 봅시다. \(\begin{aligned} p(x=1 \mid \mu)&=\mu\\ p(x=0 \mid \mu)&=1-\mu \end{aligned}\) 앞서 밀도추정에서 이야기 했듯이 밀도추정을 위해서는 확률분포가 매개변수화된 분포로 가정해야 합니다. 때문에, 이산확률변수 $x$ 에 대한 확률 분포를 표현 해야 하고, 이때 확률변수를 확률 분포로 표현하기 위해 베이누이 분포를 따른다고 가정할 수 있습니다. 즉, $p(x)$ 는 베르누이 분포로 표현 될 수 있습니다. \(\operatorname{Bern}(x \mid \mu)=\mu^{x}(1-\mu)^{1-x}\)

베르누이 분포의 기댓값, 분산

베르누이 분포의 기댓값과 분산은 다음과 같습니다.

기댓값

\[\begin{aligned} \mathbb{E}[x]&=\mu \\ &=0 \cdot(1-\mu)+1 \cdot \mu=\mu \end{aligned}\]

분산

\[\begin{aligned} \operatorname{Var}[x] &=E\left[x^{2}\right]-E[x]^{2} \\ &=\{0 \cdot(1-\mu)+1 \cdot \mu\}-\mu^{2} \\ &=\mu-\mu^{2} \\ &=\mu(1-\mu) \end{aligned}\]

가능도 함수(likelihood funciton)

이렇게 베르누이 분포를 매개변수화(parametric) 시킨 후에 우리는 확률분포의 매개변수를 찾아야 합니다. 빈도주의 관점에서는 어떤 기준(가능도 함수)를 최적화 시키는 방법을 통해 매개변수를 찾는다고 했습니다.

$x$ 값을 $N$ 번 관찰한 결과를 $\mathcal{D}=\left{x_{1}, \ldots, x_{N}\right}$ 라고 합시다. $x$ 가 독립적으로 $p(x \mid \mu)$ (매개변수 $\mu$ 가 주어졌을 때의 $x$ 가 뽑힐 확률)에서 뽑혀진다고 가정하면 다음과 같이 가능도함수(매개 변수 $\mu$ 의 함수인)를 만들 수 있습니다. \(p(\mathcal{D} \mid \mu)=\prod_{n=1}^{N} p\left(x_{n} \mid \mu\right)=\prod_{n=1}^{N} \mu^{x_{n}}(1-\mu)^{1-x_{n}}\)

빈도주의 방법

빈도주의 방법에서는 $\mu$ 값을 위 함수에서 최대화 시키는 값을 구할 수 있습니다. 이를 구하기 위해 로그 스케일 된 값에 $\mu$ 에 대한 편미분의 식을 0으로 놓고 풀면 다음과 같이 $\mu$를 구할 수 있습니다. \(\ln p(\mathcal{D} \mid \mu)=\sum_{n=1}^{N} \ln p\left(x_{n} \mid \mu\right)=\sum_{n=1}^{N}\left\{x_{n} \ln \mu+\left(1-x_{n}\right) \ln (1-\mu)\right\}\) $\mu$ 의 최대 가능도 추정치(maximum likelihood estimate)는 다음과 같습니다. \(\mu^{\mathrm{ML}}=\frac{1}{N}\sum_{n=1}^{N}{x_n}\) 위의 식처럼 정리할 수 있고, 여기서 추정된 $\mu^{ML}$ 은 표본평균 이라고도 불립니다. 데이터에서 $x=1$인 관찰값(데이터)의 수를 $m$ 이라고 하면 다음의 형태로 다시 적을 수 있습니다. \(\mu^{\mathrm{ML}}=\frac{m}{N} \text { with } m=(\text { #observations of } x=1)\) 위 식에서 주의해야 할 점은 $N$ 이 작은 경우 위 MLE(최대 가능도)는 과적합(over-fitting) 된 결과를 야기 할 수 있습니다. 예를 들어 동전을 세번 던졌는데 세번이 다 앞면이 나왔다고 가정해 봅시다. 그러면 $N=m=3$ 이고 따라서, $\mu^{ML}=1$ 이 됩니다. 이경우 최대 가능도를 따라서 다음 값들을 예측하면 무조건 앞면이 나오게 됩니다. 이러한 상황이 최대 우도법을 사용했을때 발생할 수 있는 과적합 사례입니다.

이항변수(Binary Variables) : 베이지안 방법

크기가 $N$의 데이터가 주어졌을때, 즉, 동전던지기를 $N$ 번 수행 했을때 앞면($x=1$)이 총 몇 번(확률변수)가 나왔는 지를 판단하는 문제로 고려 해봅시다. 이전에는 동전이 앞면이 나올지 뒷면이 나올지에만 관심이 있었다면, 이제는 앞면이 몇번 나올지가 궁금한 것입니다.

위에서 구한 빈도주의 관점에서 베르누이 분포와 상황이 다소 비슷하지만 우리는 동전 던지기를 했을 때 앞면이 $m$ 번 나올 수 있는 모든 경우의 수를 구해야 합니다. 즉 조합을 사용해야 합니다. 이러한 조합을 사용한 분포를 이항분포(Binomial distiribution)이라고 합니다. \(\operatorname{Bin}(m \mid N, \mu)=\left(\begin{array}{c} N \\ m \end{array}\right) \mu^{m}(1-\mu)^{N-m}\\ \left(\begin{array}{c} N \\ m \end{array}\right) \equiv \frac{N !}{(N-m) ! m !}\) 이항 분포와 베르누이 분포의 차이점을 살펴보면 앞에 조합이 추가 되었다는 점을 확인 할 수 있습니다. 조합을 사용하기 위해 기존에는 없었던 $m$이라는 매개변수가 추가 되었습니다. 즉, 빈도주위 관점과 베이지안 관점은 매개변수 차이라고 생각 할 수있습니다. 단, 여기서 $N$은 매개변수라고 생각하면 안됩니다. 주어진 데이터의 수라고 생각해야 합니다.

$N=10$ 이고 $\mu=0.25$ 일때의 이항분포 결과를 살펴 봅시다.

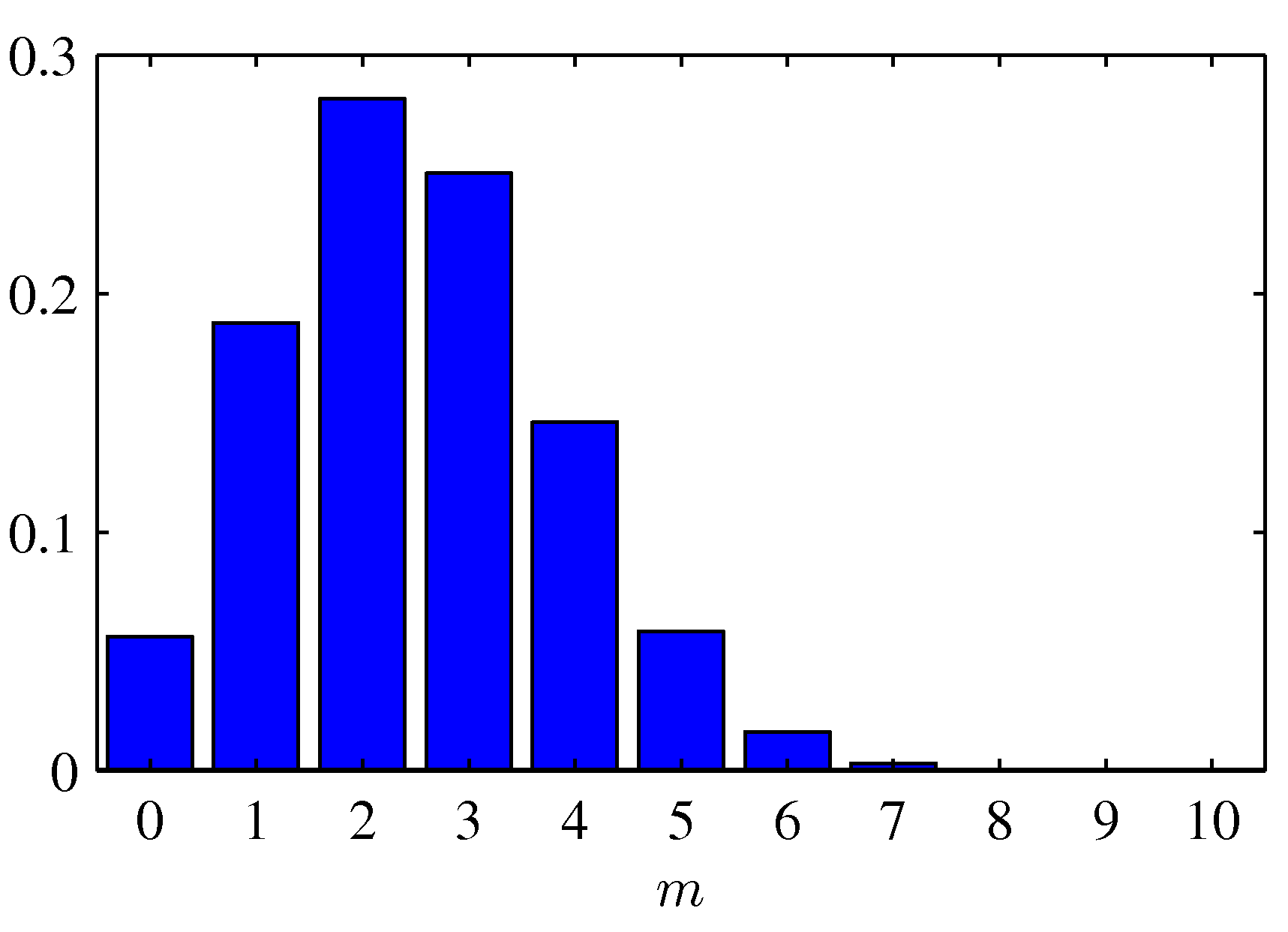
위 분포에 대한 평균과 분산은 다음과 같습니다. \(E[m] \equiv \sum_{m=0}^{N} m \cdot \operatorname{Bin}(m \mid N, \mu)=N \mu\\ \operatorname{var}[m] \equiv \sum^{N}(m-E[m])^{2} \operatorname{Bin}(m \mid N, \mu)=N \mu(1-\mu)\)

데이터를 보는 관점

빈도주의 관점과 베이지안 관점은 데이터를 바라로는 관점의 차이라고 생각 할 수 있습니다.

• 베르누이 시행의 반복: $x_{1}, \ldots, x_{N}$ 각각이 확률변수
• $x$ 가 1인 경우가 몇번 관찰 되었는가?(이항분포) : 하나의 확률 변수(관찰된 횟수) $m$

베지이안 방법을 쓰기 위해서는 데이터의 가능도를 구해야 하는데 이항분포를 가정하면 가능도 함수가 하나의 변수 $m$ 으로 ($x_{1}, \ldots, x_{N}$ 대신) 표현 가능해지므로 계산이 수훨해집니다.

베타 분포(Beta Distribution)

앞에서 이항분포에서 MLE 를 통해 얻어진 $\mu$ 의 값이 표본 평균이라는 것을 확인 했습니다. ($\mu=\bar{x}$). 문제는 이러한 빈도주의적 관점에서 샘플 결과(표본 관측 데이터)에 대해 의존적이기 떄문에 표본이 모두 앞면이 나오면 $\mu = 1$ 이되어 과적합된 결과를 얻게 됩니다.

이러한 문제를 해결하기 위해 기존의 MLE 방법이 아닌 베이지안 방식으로 매개변수를 추정하는 것을 살펴 볼 것입니다. 그 과정에서 필요한 부분은 바로 매개변수의 사전 확률 값 $p(\mu)$ 를 구하는 것입니다. 여기서 중요한점은 $p(\mu)$ 를 도입하면서 $\mu$를 상수가 아닌 랜덤 변수로 생각하는 것입니다.

MLE에서는 매개변수를 고정된 값이지만, 알지 못하는 값으로 생각하고 이를 추정하는 문제로 이를 구했습니다. 전통적 통계학에서는 이러한 방식의 한계점을 개선 하기위해 특정한 한 지점의 값이 아니라 구간 추정 방식을 도입합니다. 즉, 매개변수를 하나의 값이 아니라 어떤 범위 내에 존재 할 것이다라고 예측 하는 것입니다. 반면, 베이지안 방식에서는 매개변수를 랜덤변수로 생각하여 일반적인 확률 분포로 다루게 됩니다.

그렇다면, 매개변수가 어떤 확률 분포를 가지다면 어떤 확률 분포로 가정하는 것이 좋을 까요? 동전 던지기 문제에서는 가능도 함수의 형태가 $\mu$ 와 $\mu(1-\mu)$ 의 형태로 표현되었습니다. 베이지언 방식에서는 이 식을 전통적인 통계 방식에서 사용했던 MLE 방식이 아니라 사후 분포(posterior)를 최대화 하는 문제로 풀게 됩니다. 이때, 사후 분포는 가능도 함수로 유추된 $p(x \mid \mu)$ 와 $p(\mu)$ 의 사전 분포의 곱에 비례하게 되는 성질을 이용합니다. \(p(\mu \mid x) \propto p(x \mid \mu) p(\mu)\)

사전확률분포 = 사후확률 분포 가정

사후 분포 또한 확률 분포 입니다. 때문에 우리가 기존에 알고 있는 일반적인 형태의 분포를 가져와 계산 해야 계산이 편합니다. (예: 정규분포, 이항분포). 사전 확률 또한 확률 분포 입니다. 따라서 사전 확률 분포 또한 우리가 알고 있는 확률 분포를 근사해야 합니다. 이들을 우리가 알고 있는 확률분포로 근사하여 계산 한다고 하더라고 실제의 매개변수 분포 $p(\mu)$ (여기서는 $\mu$ 또한 확률변수라고 생각)가 어떠한 분포를 따라야하는 지는 알아 낼 수 없다.

하지만, 사전 확률의 확률 분포가 쉬운 꼴이라면, 이를 곱한 가능도 함수 또한 쉬운 확률 분포를 갖고 있을 것이다. MLE는 가능도 함수가 가장 최대화 되는 분포를 찾는 것이라고 했다. 그렇다면 사전확률과 사후확률의 분포가 같은 확률 분포의 모양을 가정(사전확률: 가우시안 분포 - 사후확률: 가우시안 분포) 한다면 어떨까? 분포의 모양이 같다면 확률값을 비교하고 계산 하는 것이 무척 쉬워질 것이다.

다시 정리하자면 가능도 함수 - 사후 확률 분포 - 사전 확률 분포가 모두 같은 분포로 표현 되어야 계산이 편리해 진다. 위에서 가능도 함수를 를 $\mu$ 와 $\mu(1-\mu)$ 의 (지수곱)형태로 표현 했다. 가능도 함수가 이와 같다면, 사후 분포(posterior) 또한 $\mu$ 와 $\mu(1-\mu)$ 의 지수곱의 형태로 표현 될 것이고, 사전 확률 또한 이런 형태로 만들어 져야 한다. 결론적으로 사전확률과 사후확률의 분포 형태가 같아지게 된다. 이러한 속성을 공액(conjugacy) 이라고 한다.

베타 분포

사실 이렇게 사전확률과 사후확률의 곱을 갖게 하는 방식은 마구잡이 방법입니다. 하지만 이렇게 할 경우 베타 분포(Beta Distribution)을 이용해서 사전확률과 사후확률의 계산을 쉽게 할 수 있습니다.

위에서 살펴 보았던 이항분포를 사용해 가능도 함수를 구하는 경우 사전 확률 분포로 베타 분포를 사용하면 베타 분포 형태의 사후 확률 분포를 얻을 수 있습니다. 이는 이항 분포와 베타 분포가 서로 공액적 관계에 놓여 있는 분포들이기 때문입니다. 즉, (베타분포 = 이항분포 $\times$ 베타분포 )와 같은 형태의 식을 얻을 수 있습니다. 베타 분포는 다음과 같습니다. \(\operatorname{Beta}(\mu \mid a, b)=\frac{\Gamma(a+b)}{\Gamma(a) \Gamma(b)} \mu^{a-1}(1-\mu)^{b-1}\) 여기에서 사용된 감마(Gamma) 함수는 다음과 같습니다. \(\Gamma(x)=\int_{0}^{\infty} u^{x-1} e^{-u} d u\) 감마함수의 주요한 특징은 계승(Factorial)을 실수로 확장시키는 성질을 지니고 있습니니다. 다음과 같이 $n$ 이 주어졌을 때 다음과 같이 Factorial 형태로 나타낼 수 있습니다. \(\Gamma(n)=(n-1) !\) 베타 분포의 기본적인 성질은 다음과 같습니다. \(\int_{0}^{1} \operatorname{Beta}(\mu \mid a, b) d \mu=1 \\ E[\mu]=\frac{a}{a+b}\\ \operatorname{var}[\mu]=\frac{a b}{(a+b)^{2}(a+b+1)}\) 위의 식에서 사용된 베타 분포는 위에서 설명한 이항 분포의 공액 분포를 설명하는 것으로, 주 확률 변수는 이항분포의 $u$ 가 됩니다. 따라서 이 베타 분포의 모수 $a, b$ 는 초모수 또는 하이퍼-파라미터(hyper parameter)라고 부르게 됩니다. 이때 hyper 의 의미는 모수(parameter)의 모수(parameter)의 의미로 모수 앞에 붙힌 것입니다. 즉, 우리가 모수를 추정하기 위해서 확률 분포를 사용하는 것처럼 모수의 확률 분포의 모양을 추정하기 위한 확률 분포를 사용하는 것을 의미합니다. 쉽게 생각하자면 추정의 추정 인 것이지요.

베타 분포의 모양은 다음과 같습니다.

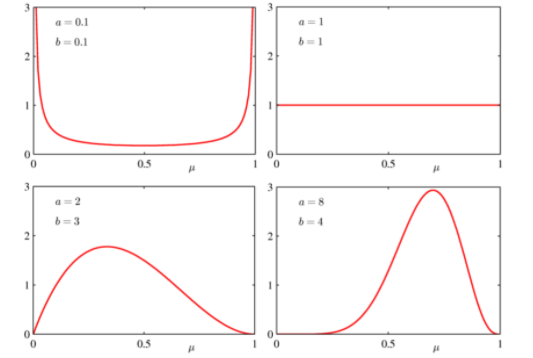
여기서 $a,b$ 를 통해 다양한 확률 분포를 만들어 낼 수 있는 것을 살펴 보았습니다. 즉, 우리가 알고 있는 사전 지식을 통해서 다양한 확률 분포를 가정 할 수 있다는 뜻이죠. 예를 들어 상황에 따라 Uniform 하게 만들 수 있거나 볼록하게 만들 수 있는 조건이 주어지게 된 것입니다.

$\Gamma(x)=(x-1) \Gamma(x-1)$ 증명

부분 적분

\[\int_{0}^{\infty} a \mathrm{~d} b=\left.a b\right|_{0} ^{\infty}-\int_{0}^{\infty} b \mathrm{~d} a\]

위의 부분적분 공식을 사용하여, 감마함수의 팩토리얼 성질을 증명 할 수 있습니다. \(\begin{aligned} a=u^{x-1} &\rightarrow \mathrm{d} a=(x-1) u^{x-2} \mathrm{~d} u\\ b=e^{-u} &\rightarrow \mathrm{d} b=-e^{-u} \mathrm{~d} u\\ \end{aligned}\)

\[\begin{aligned} \Gamma(x) &=u^{x-1}\left(-e^{-u}\right)_{0}^{\infty}+\int_{0}^{\infty}(x-1) u^{x-2} e^{-u} \mathrm{~d} u \\ &=0+(x-1) \Gamma(x-1) \end{aligned}\]

베타 분포가 normalized 임을 증명

즉, $\left(\int_{0}^{1} \operatorname{Beta}(\mu \mid a, b) \mathrm{d} \mu=1\right)$ 임을 증명하는 것을 말한다. 이때, $\int_{0}^{1} \mu^{a-1}(1-\mu)^{b-1} \mathrm{~d} \mu=\frac{\Gamma(a) \Gamma(b)}{\Gamma(a+b)}$ 을 증명하면 된다. 되냐하면 역수 관계 이기 때문이다. \(\begin{aligned} \Gamma(a) \Gamma(b) &=\int_{0}^{\infty} x^{a-1} e^{-x} \mathrm{~d} x \int_{0}^{\infty} y^{b-1} e^{-y} \mathrm{~d} y \\ &=\int_{0}^{\infty} \int_{0}^{\infty} e^{-x-y} x^{a-1} y^{b-1} \mathrm{~d} y \mathrm{~d} x \\ &=\int_{0}^{\infty} \int_{0}^{\infty} e^{-t} x^{a-1}(t-x)^{b-1} \mathrm{~d} t \mathrm{~d} x \\ &=\int_{0}^{\infty} \int_{0}^{\infty} e^{-t} x^{a-1}(t-x)^{b-1} \mathrm{~d} x \mathrm{~d} t \end{aligned}\\ \text { by } t=y+x, \mathrm{~d} t=\mathrm{d} y\)

\[\begin{array}{l} =\int_{0}^{\infty} e^{-t} \int_{0}^{\infty} x^{a-1}(t-x)^{b-1} \mathrm{~d} x \mathrm{~d} t \\ =\int_{0}^{\infty} e^{-t} \int_{0}^{1}(t \mu)^{a-1}(t-t \mu)^{b-1} t \mathrm{~d} \mu \mathrm{d} t \quad \text { by } x=t \mu, \mathrm{d} x=t \mathrm{~d} \mu \\ =\int_{0}^{\infty} e^{-t} t^{a-1} t^{b-1} t\left(\int_{0}^{1} \mu^{a-1}(1-\mu)^{b-1} \mathrm{~d} \mu\right) \mathrm{d} t \\ =\int_{0}^{\infty} e^{-t} t^{a+b-1} \mathrm{~d} t \int_{0}^{1} \mu^{a-1}(1-\mu)^{b-1} \mathrm{~d} \mu \\ =\Gamma(a+b) \int_{0}^{1} \mu^{a-1}(1-\mu)^{b-1} \mathrm{~d} \mu \end{array}\]

따라서, $\int_{0}^{1} \mu^{a-1}(1-\mu)^{b-1} \mathrm{~d} \mu=\frac{\Gamma(a) \Gamma(b)}{\Gamma(a+b)}$ 성립한다.

$\mu$ 의 사후 확률(posterior)

$\mu$ 의 사후 확률은 다음과 같이 구할 수 있습니다. 여기서 $l$ 은 전체 데이터 갯수 $N$ 에서 $m$ 의 갯수를 뺀 $N-m = l$ 을 의미 합니다. 이는 $m$에 종속적이기 때문에 이를 제외하고 계산이 가능합니다. \(\begin{aligned} P(u \mid m, e, a, b) \quad &\propto \quad & p(m, \ell \mid \mu) & \times p(n \mid a, b) \\ &= &\text{likelihood} &\times \text{prior}\\ &=&p(m \mid \mu)&\times p(\mu \mid a, b) \end{aligned}\)

\[\begin{aligned} p(\mu \mid m, l, a, b) &=\frac{\operatorname{Bin}(m \mid N, \mu) \operatorname{Beta}(\mu \mid a, b)}{\int_{0}^{1} \operatorname{Bin}(m \mid N, \mu) \operatorname{Beta}(\mu \mid a, b) \mathrm{d} \mu} \\ &=\frac{\mu^{m+a-1}(1-\mu)^{l+b-1}}{\int_{0}^{1} \mu^{m+b-1}(1-\mu)^{l+b-1} \mathrm{~d} \mu} \\ &=\frac{\mu^{m+a-1}(1-\mu)^{l+b-1}}{\Gamma(m+a) \Gamma(l+b) / \Gamma(m+a+l+b)} \\ &=\frac{\Gamma(m+a+l+b)}{\Gamma(m+a) \Gamma(l+b)} \mu^{m+a-1}(1-\mu)^{l+b-1} \end{aligned}\]

이렇게 구한 사후확률을 살펴보면 베타 분포를 따르는 것을 살펴 볼 수 있습니다. 위 식에서 $m$ 은 $x=1$ 인 경우의 횟수, $l$은 $x=0$ 인 경우의 횟수를 의미합니다. 이에 대응되는 $a$ 와 $b$ 앞면, 뒷면이 발생하는 사건에 대한 effective number of observations 입니다.

$a,b$ 모두 정수일 필요는 없습니다. 하지만, 이값은 마치 사건이 일어나기 전에 해당 사건이 발현될 횟수처럼 고려 될 수 있습니다. 따라서, $a,b$ 로 인해 지정된 횟수보다 실제 발생한 사건의 횟수가 더 적으면 사후 분포를 만들어 내는 영역에서 사전분포의 영향이 더 크게 됩니다. 반대로 실제 사건의 발생횟수가 더 커지면 가능도 함수에 의해 만들어지는 조건부 분포의 영향(사후확률)이 커진다. 결국 $a,b$를 어떻게 지정하느냐에 따라 사후 확률을 계산하는데 영향을 미치게 되는 실제 데이터의 임계크기를 결정할 수 있게 됩니다.

다음 그림을 통해 effective number의 의미를 유추 할 수 있습니다.

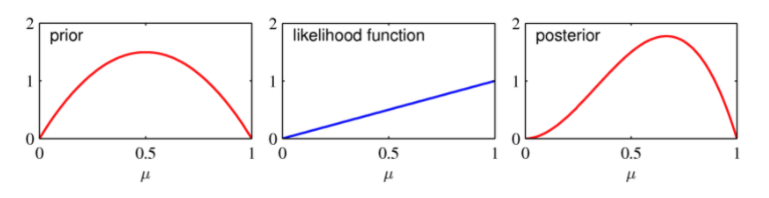
첫번째 그림(사전확률)

사전확률분포로써 $a=2, b=2$ 로 주어진 베타 분포 입니다.

두번째 그림 (가능도 함수)

$x=1$ 인 하나의 샘플에 대한 가능도 함수 입니다. \(\operatorname{Bin}(1 \mid 1, \mu)=\left(\begin{array}{l} 1 \\ 1 \end{array}\right) \mu^{1}(1-\mu)^{0}=\mu\) $x=1$ 즉, $m=1$ 인 경우의 binomial 분포를 구하면 위의 식과 같습니다. 즉, $\mu$에 대한 일차식이 이 때문에 가능도 함수 또한 선형의 형태로 나오게 됩니다.

세번째 그림 (사후 확률)

위에서 사전확률분포와 가능도 함수의 곱으로 표현 되기 때문에 중간이 볼록한 사전 확률과 오른쪽으로 치우진 그래프의 곱으로 나타내기 때문에 오른쪽으로 볼록한 그래프의 형태로 나타내게 됩니다.

위의 세개의 그래프를 통해 우리가 확인 할 수 있는 사실은 우리가 기존에 갖고 있는 사전지식(사전확률)에 새로운 데이터(가능도 함수)가 주였을 때 갱신된 결과(사후확률)을 얻을 수 있습니다.

순차적 예측 분포

순차적(Squential) 하게 확률 분포를 업데이트 하는 모델을 고려해 봅시다. 데이터가 한 건이라도 관측 될 때 마다 사후 확률을 갱신 할 있습니다. 사전분포확률과 가능도 함수의 선택은 서로 독립적이고 사전확률 분포와 사후 확률 분포의 모양이 서로 같은 함수 형태를 가지게 되므로 결국 사전 확률 분포를 이전에 결과를 통해 얻었던 사후 확률 분포를 사용해도 문제가 되지 않습니다. 이 것을 극단적으로 가정하면 다음 사건이 발생 할 때 마다 업데이트 모델을 만들 어 낼 수 있습니다.

예를 들어, 동전 던지기라면 임의로 던진 동전 한개가 앞면($x=1$) 일지 뒷면($x=0$) 일지 예측하는 문제라고 해봅시다. 물론 부가적으로 매개변수 값이 추정 되어야만 앞면과 뒷면이 나올 확률 값을 예측 할 수 있지만, 최종적으로 필요한 값은 모수값이 아니라 확률 값입니다. 이런 모델이 좋은 점은 고정된 매개변수를 선택해서 예측 하는 것이아닌(빈도주의적 관점) 매개변수 자체를 확률 변수로 놓고 영향을 줄 수 있는 모든 매개 변수의 가능성을 염두해 둔 수식을 만들어 원하는 예측값을 만들어 낼 수 있습니다.

이렇게 찾은 매개변수를 통해 우리는 특정한 조건 $x=1$ 일때의 예측 분포를 찾고자 합니다. \(p(x=1 \mid \mathcal{D})=\int_{0}^{1} p(x=1 \mid \mu) p(\mu \mid \mathcal{D}) \mathrm{d} \mu=\int_{0}^{1} \mu p(\mu \mid \mathcal{D}) \mathrm{d} \mu=\mathbb{E}[\mu \mid \mathcal{D}]\) 위 식을 보면 그냥 지금 까지 예측된 데이터로 인해 만들어진 $x$ 에 대한 평균값($\mu$)를 구하기만 하면 됐습니다.

이전에 베타 분포의 평균을 구하는 식은 다음과 같았습니다. \(E[\mu]=\frac{a}{a+b}\) 위 식을 사후 분포에 적용하면 다음과 같은 결과를 얻습니다. \(p(x=1 \mid D)=\frac{m+a}{m+a+l+b}\) 위 식에서 데이터의 수 $N=m+l$ 이 매우 커져서 $m, l \rightarrow \infty$ 이 되면 결국 이식은 MLE 결과와 동일 하게 됩니다. 즉, 사후 분포에서 사전 분포의 영향력이 작아지게 되는 것이지요

보통 데이터의 크기가 무한히 커지면 베이지안 추론방식과 MLE 의 추론 방식이 같아지는 경우가 많습니다. 데이터의 크기가 유한한 경우 MLE 로 얻어진 모수와 사전분포로 언더잊ㄴ 모수의 중간 어딘가 사후 분포로 예측한 모수값이 올 수 있게 됩니다.

데이터가 많아 질수록 사후 분포의 피크는 점점 날카롭게 됩니다. 즉, 분산이 작아지게 되고 Non-uniform 한 분포를 갖게 됩니다.